Particle in a box wave function problem

[shan564]

I have a wave function problem that I need to figure out... I have a really borderline grade, so it could mean the difference between an 'A' and a 'B' in my graduate Modern Physics class.

Basically, I have to figure out the wave function and the transmission and reflection coefficients. My professor did a really crappy job of explaining this stuff in class, so I'm totally lost.

Here's the question:
Consider a potential with the following shape:

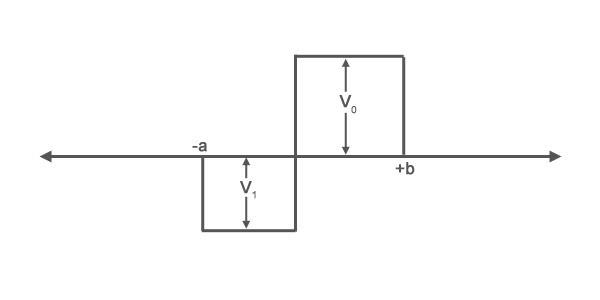
What are the wave functions for all regions of the problem is a particle beam approaches the barrier from negative infinity with an energy E? Find the reflection and transmission coefficients.

 

[dwintz02]

Start by breaking down the potential into 4 parts, and solving the Schrodinger equation for each.

 

[shan564]

That's what I thought I'm supposed to do, but I'm not sure if I'm doing it right. Does that mean that I need to plug it into psi(x) = [(2/L)^(1/2)] [sin(n*pi*x/L)] ? My professor didn't do a very good job of explaining Schrodinger's equation, so I don't have a very thorough understanding of it.

Also, does "reflection" and "transmission" coefficients just mean that I need to plug it into these equations?
http://upload.wikimedia.org/math/0/f/2/0f28f1a66cd127802853761235a4ffaf.png
http://upload.wikimedia.org/math/0/f/2/0f28f1a66cd127802853761235a4ffaf.png

 

[dwintz02]

The Schrodinger equation, among many things, gives you a differential equation for Psi, of which, based on your potential energy, you can solve for Psi. I'd look it up on Wikipedia (you want the time independent form) so you can get practice solving it (it's actually not that bad for the potentials given). And for the reflection and transmission coefficients, those will not be the answer. Those are for a different potential (a single finite barrier I think, but that's just an inspective guess.)

 

[Avodyne]

You have four regions: x<-a, -a<x<0, 0<x<b, and x>b, which I will call R1, R2, R3, and R4. In each region, you solve the time-independent Schr eq. For a consant potential, the most general solution is of the form A e^(ikx) + B e^(-ikx), except possibly in R3; the solution is of this form if E>V0, but takes the form A e^(kx) + B e^(-kx) if E<V0. The value of k is generally different in each region, so you should give them all different names (eg, k1, etc.). You should figure out what they are; for example, you should find $k_1=k_4=(2mE/\hbar^2)^{1/2}$.

Next, you are doing a scattering problem with a particle incident from the left, so in R4 the particle should only be moving to the right; that means, in R4, the solution must be of the form G e^(i k4 x).

In R1, there is the incident wave, and a reflected wave, so we should take the wave function to be A e^(i k1 x) + B e^(-i k1 x). The reflection coefficient will then be R=|B|^2/|A|^2. The transmission coefficient will be T=|G|^2/|A|^2.

In R2 and R3, we use C e^(i k2 x) + D e^(-i k2 x) and E e^(i k3 x) + F e^(-i k3 x) (for the E>V0 case; if you solve this one, you can get the solution to the E<V0 case by letting k3 be imaginary, but you must know whether it's real or imaginary before taking absolute values to get R and T).

Now, at each of three boundaries between regions (x=-a, x=0, and x=b), the wave function and its first derivative must match. You can save yourself a lot of trouble by solving this ONCE: consider a match between A e^(i k x) + B e^(-i k x) on the left and C e^(i k' x) + D e^(-i k' x) on the right, at x=L. This will give you two equations that relate A and B to C and D. It's useful to write these in matrix form:
$$\begin{pmatrix} A \\ B \end{pmatrix}=\begin{pmatrix} \ldots & \ldots \\ \ldots & \ldots \end{pmatrix}\begin{pmatrix} C \\ D \end{pmatrix}$$
where the entries in the square matrix will depend on k, k', and L.

Now do this at each boundary, writing the column vector (A,B) as a matrix times (C,D), then (C,D) as a matrix times (E,F), then (E,F) as a matrix times (G,0). Then you can write (A,B) as the product of three matrices times (G,0). Multiply out the three matrices, and you have A as something times G, and B as something times G. G then cancels out when you compute R=|B|^2/|A|^2 and T=|G|^2/|A|^2, so you might as well just set G=1.

And you're done!

 

[shan564]

Thanks a lot! So basically, the first step is to figure out each k and solve the equation for psi? I guess that k2 and k3 are the same as k1 and k4, except that I replace "E" with "V-E", right?

 

[Gokul43201]

Thanks a lot! So basically, the first step is to figure out each k and solve the equation for psi? I guess that k2 and k3 are the same as k1 and k4, except that I replace "E" with "V-E", right?

The values of k come from solving the (Time Independent) SE. k1 and k4 will be the same, but k2 and k3 will have one or two (depending on how big E is) important differences.

 

[shan564]

Multiply out the three matrices, and you have A as something times G, and B as something times G.

OK... I got this far and I corroborated my answer with a classmate's.

Here's my latest problem... I multiplied out the three matrices using Mathematica and result (the "something" mentioned above in bold) was ridiculously long. I was expecting some of the things to cancel out, but it didn't seem to work out that way. This answer seems too complicated... am I doing something wrong or is this it?

 

[dwintz02]

It should be pretty long, especially since you're transmitting through different potentials, with different signs, and with different widths--doesn't leave much room for things to cancel out. I can't say for sure whether or not your answer is correct, but that it should be long.