Number2Pencil
- 204
- 1
This is more of a "help me understand" than "help me find the answer" problem. forgive me for not using the template.
this is the "little r-e" model, similar to the hybrid model
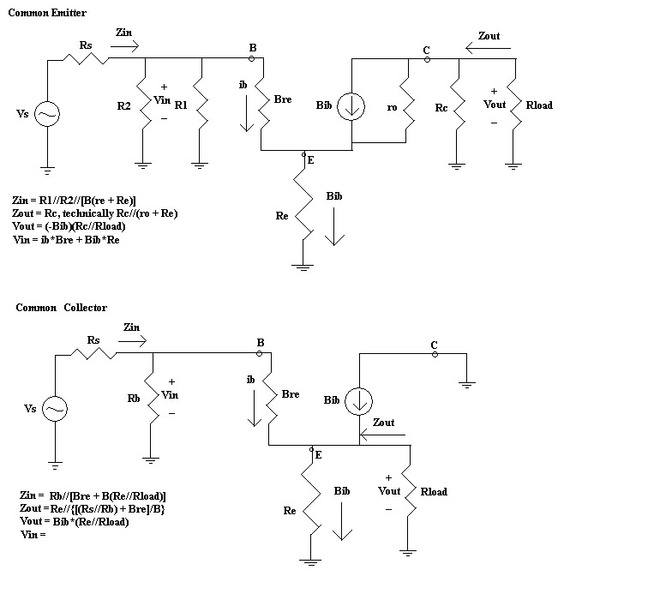
I'm having a bit of trouble understanding how my professor got the equations for these two examples.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Common Emitter:
/////////////////////////////
Zin: why does Re get multiplied by Beta?
Why does he not consider ro, Rc, or Rload?
Zout: Why does he not consider Bre, R1, R2, or Rs?
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Common Collector:
/////////////////////////////
Zin: once again, Beta being multiplied by what is connected to the emitter?
Zout: now he DOES consider all the resistors on the left, AND divides it by Beta.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
attempt
/////////////////////////////
I think I can see why Re is being multiplied by Beta in the common emitter. The current going through Bre is ib and the current going through Re is Bib, so apparently there needs to be a multiplying factor of Beta to make up for it...for what reason, I have no clue.
this is the "little r-e" model, similar to the hybrid model
I'm having a bit of trouble understanding how my professor got the equations for these two examples.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Common Emitter:
/////////////////////////////
Zin: why does Re get multiplied by Beta?
Why does he not consider ro, Rc, or Rload?
Zout: Why does he not consider Bre, R1, R2, or Rs?
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Common Collector:
/////////////////////////////
Zin: once again, Beta being multiplied by what is connected to the emitter?
Zout: now he DOES consider all the resistors on the left, AND divides it by Beta.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
attempt
/////////////////////////////
I think I can see why Re is being multiplied by Beta in the common emitter. The current going through Bre is ib and the current going through Re is Bib, so apparently there needs to be a multiplying factor of Beta to make up for it...for what reason, I have no clue.
Last edited: