- #1
mitleid
- 56
- 1
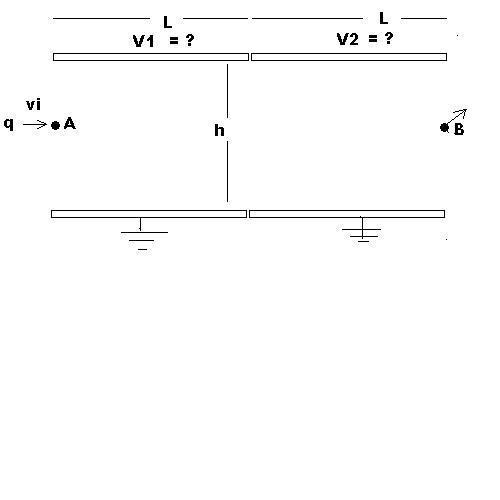
Two adjacent parallel plate capacitors are used to deflect charged particles as shown in the figure. The relevant dimensions l and h are shown. The lower capacitor plates are grounded while the upper plates are kept at some voltages V1 and V2, which are to be found in this problem given the following.
A positively charged particle q with mass m enters horizontally at point A. After executing some trajectory, the particle exits at point B, which has the same vertical position as point A. However, the velocity at B is not horizontal, and has some component Vy. What are the potentials? Neglect the effects of gravity.
Some relevant equations :
F = qE
Acceleration (a) = F / m = qE/m
mechanics:
x = Vi*t
y = - (qE/2m)t^2
Vfx = Vi
Vfy = -(qE/m)*(1/Vi)
I think I have most of what I need here. This next figure illustrates how I think the two trajectories take place, and I wanted to check this before I went further.

Since the bottom plates are grounded, voltage across them is equal to 0. E points from higher to lower potentials, so the field would expected to be downwards.
A downward field would correspond to the first hypothetical trajectory. However, for Vy to be "positive" or upwards, an upward field would have to take place for the second trajectory. Thus V = 0 would have to be higher than V2, making it negative or also equal to 0.
Am I headed in the right direction?
A positively charged particle q with mass m enters horizontally at point A. After executing some trajectory, the particle exits at point B, which has the same vertical position as point A. However, the velocity at B is not horizontal, and has some component Vy. What are the potentials? Neglect the effects of gravity.
Some relevant equations :
F = qE
Acceleration (a) = F / m = qE/m
mechanics:
x = Vi*t
y = - (qE/2m)t^2
Vfx = Vi
Vfy = -(qE/m)*(1/Vi)
I think I have most of what I need here. This next figure illustrates how I think the two trajectories take place, and I wanted to check this before I went further.
Since the bottom plates are grounded, voltage across them is equal to 0. E points from higher to lower potentials, so the field would expected to be downwards.
A downward field would correspond to the first hypothetical trajectory. However, for Vy to be "positive" or upwards, an upward field would have to take place for the second trajectory. Thus V = 0 would have to be higher than V2, making it negative or also equal to 0.
Am I headed in the right direction?