Find Center of Mass: Calculate x,y Coordinates with R = sum(m*r)/sum(m)

AI Thread Summary
To find the center of mass coordinates (x,y) for the object with varying densities, the approach involves breaking the object into three rectangles. Each rectangle's mass and center of mass must be calculated separately. After determining the individual centers, the overall center of mass can be found by treating these centers as point masses. The formula R = sum(m*r) / sum(m) is applicable for this calculation. This method simplifies the problem and provides a clear path to the solution.
xxlvh
Messages
9
Reaction score
0
1. The density of part A (p)(kg/m^3) and in part B (p/2)(kg/m^3). Find the coordinate (x,y) of the center of mass of this object.

jip568.gif

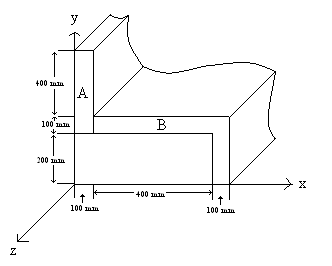
(consider a piece of the object that is one meter in the z direction)

2. R = sum(m*r) / sum(m)...maybe? I am completely stumped on how to start this problem my teacher has done no sample problems that are anything like this, not even anything in 3D, if anyone could at least provide a hint to get me started on this one? Would be greatly appreciated.
 
Last edited:
Physics news on Phys.org
This isn't a 3d problem, it's a 2d problem and he only wants (\overline x,\overline y) Break it up into three rectangles, find the mass and center of mass of each. Then find the center of mass of the three masses as if they were point masses at their centers of mass.
 
Awesome, thanks a ton for helping me get started!
 
Thread 'Have I solved this structural engineering equation correctly?'

Thread 'Have I solved this structural engineering equation correctly?'

Hi all, I have a structural engineering book from 1979. I am trying to follow it as best as I can. I have come to a formula that calculates the rotations in radians at the rigid joint that requires an iterative procedure. This equation comes in the form of: $$ x_i = \frac {Q_ih_i + Q_{i+1}h_{i+1}}{4K} + \frac {C}{K}x_{i-1} + \frac {C}{K}x_{i+1} $$ Where: ## Q ## is the horizontal storey shear ## h ## is the storey height ## K = (6G_i + C_i + C_{i+1}) ## ## G = \frac {I_g}{h} ## ## C...
View full post »

Similar threads

Center of mass and momentum- A question about systems
Replies
25
Views
1K
Engineering Calculating the mass of air in a pressurised air tank
Replies
14
Views
3K
Fidning the center of mass of an incomplete circle
Replies
4
Views
3K
Center of mass of spherical shell inside of cone (Apostol Problem).
Replies
3
Views
2K
Calculate the speed and angle of the center of mass before a collision
Replies
3
Views
909
Finding the center of mass of a simple 2D shape
Replies
9
Views
3K
I Question about the velocity of the center of mass reference frame
Replies
21
Views
2K
Finding the center of mass of a solid hemisphere
Replies
19
Views
3K
What is the distance R between centers of mass in a barbell-shaped object?
Replies
9
Views
1K
Finding the POSITION of the center of mass
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top