- #1
Axecutioner
- 32
- 0
Problem:
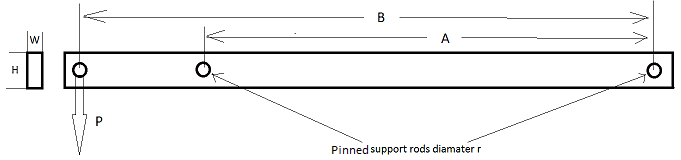
What is the equation that relates properties of a metal (modulus of elasticity, yield strength, elongation, etc) to how far it can deflect before permanently being bent. I can calculate how far a beam will deflect under different loading and support but I just don't know what the limit is until it won't bounce back to it's original state again. I'm looking at 6061-T6 aluminum.
I've found two different equations online:
σ = F/A
F = EI∏^2 / (KL)^2
I want to say it's σ = F/A but I would think that orientation of the beam would matter. It would be easier to bend it about it's width than it's height. I would also think that in this case, if B was longer it would require a smaller P value to bend the beam.
I'm trying to teach myself this stuff for a project and I won't be learning it in college classes until Fall quarter so any help will be appreciated! Thanks
What is the equation that relates properties of a metal (modulus of elasticity, yield strength, elongation, etc) to how far it can deflect before permanently being bent. I can calculate how far a beam will deflect under different loading and support but I just don't know what the limit is until it won't bounce back to it's original state again. I'm looking at 6061-T6 aluminum.
I've found two different equations online:
σ = F/A
F = EI∏^2 / (KL)^2
I want to say it's σ = F/A but I would think that orientation of the beam would matter. It would be easier to bend it about it's width than it's height. I would also think that in this case, if B was longer it would require a smaller P value to bend the beam.
I'm trying to teach myself this stuff for a project and I won't be learning it in college classes until Fall quarter so any help will be appreciated! Thanks