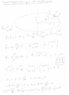- #1
Ulrich
- 24
- 0
I recently saw a documentary, which claimed that if the Earth rotation slows down the water of the oceans will flood to the north and south because the centripetal force at the equator diminishes. In fact, earth’s radius is about 20 km longer at the equator than at the poles. However, I doubt that any water would be displaced because the Earth is not solid in the interior and the crust is by far too thin to hold the earth’s original ellipsoidal form. So I think that all the water would stay at the same place with less rotation.
On the other hand, I calculated the equatorial radius for the actual angular velocity. It should only be about 10 km longer than the polar radius, which means, if the calculation is right, that the solid crust is effectively slow in adapting its form to a decrease in angular velocity ω. However, my calculation may be wrong. Here is what I did: assuming that the Earth is covered with water, there are three forces acting on a small volume of water with mass m at the surface. The first is the support force S perpendicular to the surface and therefore to the derivative of a curve y(x) to be determined delimiting the surface in Cartesian coordinates. The second is the gravitational force G pointing to earth’s center and the third is the centripetal force Z perpendicular to the rotation axis. All vector forces are supposed to be in equilibrium (no flow of water) so we have S + G + Z = 0, which yields the differential equation [itex]\left(x^2+y^2\right)^{3/2}=\frac{G M}{ω^2}\left(\frac{y' y}{x}+1\right)[/itex], where G is the gravitational constant and M the mass of the Earth. It’s solution is a curve near to an ellipse for small ω. You can see the maths in the Mathematica file in the attachement.
I am sure that I did the maths correctly but something may be wrong with the equilibrium of the forces. I would greatly appreciate any comments.
On the other hand, I calculated the equatorial radius for the actual angular velocity. It should only be about 10 km longer than the polar radius, which means, if the calculation is right, that the solid crust is effectively slow in adapting its form to a decrease in angular velocity ω. However, my calculation may be wrong. Here is what I did: assuming that the Earth is covered with water, there are three forces acting on a small volume of water with mass m at the surface. The first is the support force S perpendicular to the surface and therefore to the derivative of a curve y(x) to be determined delimiting the surface in Cartesian coordinates. The second is the gravitational force G pointing to earth’s center and the third is the centripetal force Z perpendicular to the rotation axis. All vector forces are supposed to be in equilibrium (no flow of water) so we have S + G + Z = 0, which yields the differential equation [itex]\left(x^2+y^2\right)^{3/2}=\frac{G M}{ω^2}\left(\frac{y' y}{x}+1\right)[/itex], where G is the gravitational constant and M the mass of the Earth. It’s solution is a curve near to an ellipse for small ω. You can see the maths in the Mathematica file in the attachement.
I am sure that I did the maths correctly but something may be wrong with the equilibrium of the forces. I would greatly appreciate any comments.
Attachments
Last edited: