2D Elastic collision of varying mass, velocities, and angles

[Samuelriesterer]

Problem statement:
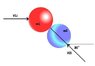
Two pucks of radius 0.05 meters collide as shown in attached picture.

The mass of puck 1 is 0.1 kg and that of puck 2 is 0.15 kg. The initial velocities are v1i = 1 m/s and v2i= 0.6 m/s. (1) Assuming no friction between the pucks, only normal forces during collision, in what direction is the acceleration for each puck during collision?

Relative equations:
m1v1i_x + m2v2i_x = m1v1f_x + m2v2f_x
m1v1i_y + m2v2i_y = m1v1f_y + m2v2f_y
½ m1v1i + ½ m2v2i = ½ m1v1f + ½ m2v2f

Work done so far:
1) In what direction is the acceleration for each puck during collision

Both are accelerating toward the center of the pucks during the collision phase

2) Choose your coordinate axes to be in the direction of the acceleration and perpendicular to it. Determine the components of the original velocities along these axes.

We will choose a coordinate system that places the x-axis along the pucks’ centers of mass and the y-axis perpendicular to the x-axis and through the center of collision.

V1i_x = V1i cos (θ) v1i_y = v1i sin (θ)
v2i_x = -v2i v2i_y = 0

(3) What happens to the velocity components perpendicular to the line between centers?

The components perpendicular to the line between the centers (i.e. the y axis) remain the same while the x components change signs.

(4) For the components in the direction of the acceleration, use momentum and kinetic energy conservation to determine the final values for these components. {You could use the center of mass frame here.}

I will use a constant of q = 3/2 to change the equations of momentum conservation and KE conservation:

m1v1i_x + m2v2i_x = m1v1f_x + m2v2f_x →
(m1)(v1i_x) + q(m1)(v2i_x) = (m1)(v1f_x) + q(m1)(v2f_x) →
(v1i_x) + q(v2i_x) = (v1f_x) + q(v2f_x) →
(v1i_x) + q(v2i_x) = (v1f_x) + q(v2f_x) →
V1i cos (θ) + q(-v2i) = (v1f_x) + q(v2f_x)

½ (m1)(v1i^2) + ½ q(m1)(v2i^2) = ½ (m1)(v1f^2) + ½ q(m1)(v2f^2) →
(v1i^2) + q(v2i^2) = (v1f^2) + q(v2f^2)

Not sure at this point on how to solve this system.

(5) Combine the results from (3) and (4) to find the final velocities for both pucks.

 

[haruspex]

1) In what direction is the acceleration for each puck during collision

Both are accelerating toward the center of the pucks during the collision phase

Not sure what that means... do you mean towards the point where they touch?
Consider the blue puck. What is the direction of the impulse applied by the red puck?

 

[Samuelriesterer]

I mean if we draw a line through the centers then the forces during collision would be along that line. At least this is what I think my teacher means because he says the acceleration is along the x-axis on that line through the centers. I am not sure on how that works though.

 

[haruspex]

I mean if we draw a line through the centers then the forces during collision would be along that line.

Yes.

(v1i_x) + q(v2i_x) = (v1f_x) + q(v2f_x) →
V1i cos (θ) + q(-v2i) = (v1f_x) + q(v2f_x)

Don't do that last step - keep it in terms of the x components.

(v1i^2) + q(v2i^2) = (v1f^2) + q(v2f^2)

You need an equation for the y components so that you can reduce the energy equation to only mention the x components.

 

[Samuelriesterer]

I didn't think you could isolate components in the conservation of KE equation. But would it look something like this:

$(v1i_x) + q(v2i_x) = (v1f_x) + q(v2f_x)$
$(v1i_y) + q(v2i_y) = (v1f_y) + q(v2f_y)$

$½ (m1)(v1i^2) + ½ q(m1)(v2i^2) = ½ (m1)(v1f^2) + ½ q(m1)(v2f^2) →$
$(v1i^2) + q(v2i^2) = (v1f^2) + q(v2f^2) →$
$\sqrt{(v1i_x^2 + v1i_y^2)} + q\sqrt{ (v2i_x^2 + v2i_y^2)} = \sqrt{ (v1f_x^2 + v1f_y^2)} + q\sqrt{ (v2f_x^2 + v2f_y^2)}$

 

[haruspex]

I didn't think you could isolate components in the conservation of KE equation

As a matter of principle, you can't, and I was not suggesting you could. There may be external forces which convert KE in one direction to KE in another. I meant you to apply conservation of momentum in the y direction. However, in the absence of external forces it (usually?) turns out that KE is preserved independently in the two directions.

$(v1i^2) + q(v2i^2) = (v1f^2) + q(v2f^2) →$

Now collect the q terms on one side, the other terms on the other side, and factorise both sides.
Use the conservation of momentum equation to eliminate a factor.
You should end up with a standard equation that only relates the before and after velocities in the x direction. The relative masses disappear. (In its more general form, i.e. with some loss of KE, it is known as Newton's Experimental Law.)

 

[mo_0820]

I mean if we draw a line through the centers then the forces during collision would be along that line. At least this is what I think my teacher means because he says the acceleration is along the x-axis on that line through the centers. I am not sure on how that works though.

The forces during collision along the orientation of the line through the centers, the impulse during collision is olong this orientation, so the puck 2 should move along the opposite orientation of $\boldsymbol{v_2}$.
Plus this, you may completely solve this problem.

 

[Samuelriesterer]

If you guys are seeing something I am not please speak a little more plainer. I don't see how to solve the system of equations:

(v1i_x) + q(v2i_x) = (v1f_x) + q(v2f_x)
(v1i_y) + q(v2i_y) = (v1f_y) + q(v2f_y)

(v1i^2) + q(v2i^2) = (v1f^2) + q(v2f^2) →
(v1i_x + v1i_y) + q(v2i_x + v2i_y) = (v1f_x + v1f_y) + q(v2f_x + v2f_y)

I could eliminate q by factoring but that doesn't help.

 

[mo_0820]

I mean add this equation
$|\frac{v2f_y}{v2f_x}|=|\frac{v2i_y}{v2i_x}|$.

 

[haruspex]

(v_1i²) + q(v_2i²) = (v_1f²) + q(v_2f²) →

You didn't do what I said. Collect all the terms involving q on one side, all others on the other side, then factorise each side. Do you know how to factorise a²-b²?

 

[mo_0820]

Follow you, at last you got a equation by two unknown variables, so you get a relation but cann't solve it.
Then you should find another equation for resolving it.

 

[Samuelriesterer]

Do you know how to factorise a2-b2?

Yes I know how to factor that: (a-b)(a+b). Do you mean to use the conservation of momentum equation in its non-component form? That is:

q(v2i - v2f) = v1f - v1i

I'm sorry I still don't see a solution much less a way to bring it back to component form.

 

[haruspex]

Yes I know how to factor that: (a-b)(a+b). Do you mean to use the conservation of momentum equation in its non-component form? That is:

q(v2i - v2f) = v1f - v1i

I'm sorry I still don't see a solution much less a way to bring it back to component form.

Here's what I've asked you to do:
(v_1i²) + q(v_2i²) = (v_1f²) + q(v_2f²)
(v_1i²) - (v_1f²) = q{(v_2f²) - (v_2i²)}
Can you see that both sides have expressions of the form a²-b²?
Having factored them, can you see that you have one of the factors each side in your momentum equation?

 

[Jazz]

@Samuelriesterer @haruspex

Could I ask one question about this problem?

As fas as I understand, the unknowns are:

$v_1'$, $\theta_1'$, $v_2'$ and $\theta_2'$ (The prime symbol $(')$ stands for final values).

By assuming conserved quantities, we can have 3 equations (2 from conservation of momentum (x and y axis) and one from conservation of KE)

Where is the other equation coming from? Or what am I not taking into account?

Thanks !

 

[Samuelriesterer]

@Jazz - All the initials are known (see attached picture). The finals are unknown.

@haruspex - I worked the KE down after factoring at got:

(V1i-v2i) = (v2f-v1f)

But my textbook says not to use this equation or 2D collisions.

 

[Jazz]

@Jazz - All the initials are known (see attached picture). The finals are unknown.

I'm indeed referring to finals values (I meant that by the prime symbol).

 

[Samuelriesterer]

Yes sorry I see that now.

 

[haruspex]

@haruspex - I worked the KE down after factoring at got:

(V1i-v2i) = (v2f-v1f)

But my textbook says not to use this equation or 2D collisions.[/QUOTE]
You can use it applied to the velocity components along the line of collision (i.e. normal to the surfaces in contact), but not to the velocities as wholes.

 

[mo_0820]

You guys can not see my replies or something?
@Jazz
No friction, and the $\boldsymbol{F}$ through the centers, so $\theta$s are all constant.
The unknown four variables are $\boldsymbol{v1_f}$ and $\boldsymbol{v2_f}$, due to 2D problem.
Now we find the other equation
$\boldsymbol{F} // \vec{OO'}$
$\Delta\boldsymbol{p}_1, \Delta\boldsymbol{p}_2 // \vec{OO'}$ or $\Delta\boldsymbol{v}_1, \Delta\boldsymbol{v}_2 // \vec{OO'}$
For this situation, I think $\boldsymbol{v}_{2i} // \vec{OO'}$, so it's simpler to use $\Delta\boldsymbol{v}_2 // \vec{OO'}$ than $\Delta\boldsymbol{v}_1 // \vec{OO'}$.

 

[haruspex]

You guys can not see my replies or something?

I see them, but can't make much out of them.

No friction, and the F through the centers, so θs are all constant.

Depends what they mean. If θ₁ denotes the direction of travel of the incoming puck, that changes. The other doesn't have a defined prior direction.
Your post #7 merely seemed to confirm what had been said in post #3.
This equation looks most odd, seems to be dividing by vectors:

$|\frac{v2f_y}{v2f_x}|=|\frac{v2i_y}{v2i_x}|$

.
Where do you get that from?

 

[mo_0820]

Depends what they mean. If θ₁ denotes the direction of travel of the incoming puck, that changes. The other doesn't have a defined prior direction.

I think $\theta$s are angular displacement, see

As fas as I understand, the unknowns are:

$v_1'$, $\theta_1'$, $v_2'$ and $\theta_2'$ (The prime symbol $(')$ stands for final values).

Your post #7 merely seemed to confirm what had been said in post #3.
This equation looks most odd, seems to be dividing by vectors

Yes.
If $\boldsymbol{v}_{2i} // \vec{OO'}$ and $\Delta\boldsymbol{v}_2 // \vec{OO'}$,
then $\boldsymbol{v}_{2f} // \boldsymbol{v}_{2i} // \vec{OO'}$, and so on.

 

[haruspex]

I think $\theta$s are angular displacement, see

I read Jazz's post differently.
You cannot divide by a vector. Please define your vec1//vec2 notation (I presumed it meant 'component of vec1 in the direction of vec2').

 

[mo_0820]

vec1 // vec2 means they have the same or opposite orientation.
They are parallel.

 

[mo_0820]

I see, please forgive my poor English, anyway.
I didn't divide by a vector.

 

[Samuelriesterer]

The problem question states how we have to answer the questions. So there is a specific way to do this. I.e. COE and COM. The reason I think this problem is solvable with 4 unknowns and 2 equations is that we are assuming that the y components remain the same as the initial values, at least that is how I read the problem.

 

[haruspex]

The problem question states how we have to answer the questions. So there is a specific way to do this. I.e. COE and COM. The reason I think this problem is solvable with 4 unknowns and 2 equations is that we are assuming that the y components remain the same as the initial values, at least that is how I read the problem.

Not sure if I've confused you by not being careful about total velocity versus velocities in the x direction.
As you wrote in the OP, nothing interesting happens in the y direction. The velocities don't change, so the momentum doesn't change, and the portion of the KE that's in that direction doesn't change. Since the collision as a whole is perfectly elastic, the contribution to the KE from motion in the x direction is also preserved. This reduces the problem to a 1-D collision.
You may still be puzzled how it is possible to determine four unknowns from only two equations. In fact you have three obviously - two for linear momentum and one for energy - plus, effectively, another equation from the absence of friction.

 

[Samuelriesterer]

Im confused at this point, yes. I'm almost giving up, I've been thinking about this problem for days now and become too obsessed.

I thought that because the Y components don't change in the final velocities that those would not be unknowns.

Also, how or do I need to change the 1d collision result back to a 2d collision? Does it involves something about the axis being rotated?

 

[haruspex]

I thought that because the Y components don't change in the final velocities that those would not be unknowns.

That's an equivalent way of looking at it. With that view you have two equations and two unknowns.

how or do I need to change the 1d collision result back to a 2d collision?

Just add the velocities together vectorially.

 

[Jazz]

What would it be the reason to assume that the components of the velocities in the y direction don't change at all? It's clear to me that their directions along the axis remain the same, but not their magnitudes.

I've found their final velocities but I can't find a way to come up with their angles (It would be great if Samuelriesterer could post the answer to make sure I didn't make a mistake).

Im confused at this point, yes. I'm almost giving up, I've been thinking about this problem for days now and become too obsessed.

I thought that because the Y components don't change in the final velocities that those would not be unknowns.

Also, how or do I need to change the 1d collision result back to a 2d collision? Does it involves something about the axis being rotated?

I was also lost around the geometry to tackle this problem. Maybe treat CoM as a whole and forget the x and y components can be more meaningful.

We start assuming the impulse experienced by both pucks is the same and the KE of the system is conserved:

$Imp_1 = Imp_2$

$\Delta t F_1 = \Delta t F_2$

$F_1 = F_2$

$m_1\left(\frac{\Delta v_1}{\Delta t}\right) = m_2\left(\frac{\Delta v_2}{\Delta t}\right)\hspace{35pt}$ <-- Prime $(')$ for final quantities.

$m_1\left(\frac{v_1'-v_1}{\Delta t}\right) = m_2\left(\frac{v_2' -v_2}{\Delta t}\right)$

$m_1(v_1'-v_1) = m_2(v_2' -v_2)\hspace{35pt}$ <-- CoM

$\frac{m1}{m_2} = \frac{v_1'-v_1}{v_2' -v_2}\hspace{35pt}(1)$

If I'm not wrong, we have the two equations that allow us to solve for these two unknowns, without having made any assumptions about what happens along the x or y-axis (which it's a neat thing to me :) ).

In $(1)$ you have two unknowns. Just solve for one of them and use CoE to find the other one.

 

[haruspex]

What would it be the reason to assume that the components of the velocities in the y direction don't change at all?

The impulse that each gives to the other is along the x axis. Apply conservation of momentum separately to each ball along the y axis.