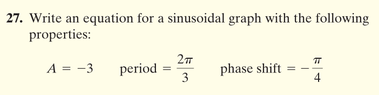7.t.27 Write an equation for a sinusoidal graph with the following properties:

[karush]

$\tiny{7.t.27}$
$\textsf{Write an equation for a sinusoidal graph with the following properties:}\\$
$$A=-3,
\textsf{Period}=\frac{2\pi}{3},
\textsf{Phase Shift}=-\frac{\pi}{4}$$
\begin{align*}\displaystyle
A&=-3\\
T&=\frac{2\pi}{3}=\frac{2\pi}{\omega}\\
\omega&=3\\
PS&=-\frac{\pi}{4}=\frac{\phi}{\omega}\\
\phi&=\pi
\end{align*}
\begin{align*}\displaystyle
y_{27}&=A\sin{\left[\omega\left(x-\frac{\phi}{\omega} \right)\right]}
\end{align*}
$\textit{so then}$
\begin{align*}\displaystyle
Y_{27}&=-3\sin{\left[3\left(x-\frac{\pi}{12} \right)\right]}
\end{align*}

hopefully

 

[MarkFL]

The amplitude of a sinusoidal function is one-half the vertical distance between the minimum and maximum, and so should never given as a negative value. Given:

$$y=A\sin\left(\omega(x-\phi)\right)\tag{1}$$

The amplitude is then $|A|$. Thus, both of the following have an amplitude of 3 units:

$$y=3\sin(x)$$

$$y=-3\sin(x)$$

You have the correct angular velocity $\omega$, but in (1) the phase shift is $\phi$ and so $\phi$ will have the opposite sign of the value given for the phase shift:

$$y=3\sin\left(3\left(x-\left(-\frac{\pi}{4}\right)\right)\right)=3\sin\left(3\left(x+\frac{\pi}{4}\right)\right)$$

 

[karush]

View attachment 6987

here is what was given...

 

[MarkFL]

here is what was given...

My mind must've been on something other than this problem when I posted last night...$A=-3$ is not saying the amplitude is -3...so what I would give is:

$$y=-3\sin\left(3\left(x+\frac{\pi}{4}\right)\right)$$

Sorry for the confusion. :D