Air pressure question for two different water columns

[Colin Wilson]

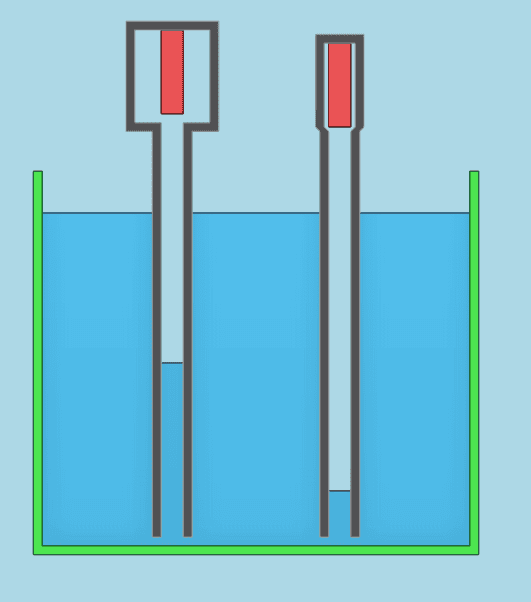
If you had pressure sensors (red) inside closed containers (black). The one on the left having more air volume than the one on the right. They are inside a bucket (green) that is filled with water. The water will rise higher in the left container. Will the pressure sensor readings be identical or will the right one read higher?

 

[Orodruin]

The pressure in the gas will be the same as that at the liquid surface inside the tube.

 

[Baluncore]

The right pressure sensor will read a higher pressure.
It is able to push water further downwards than the sensor on the left.