- #1
- 1,106
- 620
- TL;DR Summary
- Possible condition for maximum deflection during collision
Large mass (M) - moving - collides elastically with stationary small mass (m) as per crude diagram below. Angle θ is formed between the initial path of the large mass and the line of centres during collision. I would like to say that maximum deflection of the large mass occurs when cos(θ)=m/M so that the small mass 'stops' the incoming component of momentum along line of centres leaving the large mass with only the component perpendicular to line of centres. Is this correct thinking ?
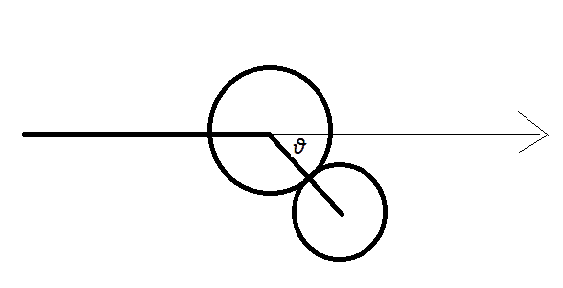
Last edited: