- #1
- 2,355
- 10
BRS: Those Damnable "Paradoxes". I. Overview
I hate talking about them! But I will force myself to try anyway.
What am I talking about? The so-called Bell spaceship "paradox" and Ehrenfest rotating disk "paradox". These paradoxes seem to come up every six to twelve months in PF, and always seem to lead to extremely long and thoroughly confused threads. As the discussion becomes increasingly heated and circular, the frequent result is that a Mentor locks the thread, and some of the disputants have even been banned from PF. These are not good outcomes.
Therefore, I think it will be useful to SA/Ms who regularly post in the relativity or astrophysics forums to have a place where we can show/discuss all the math and all the pictures without fear of interruption from possibly well intentioned newbies--- or even worse, from cranks. Without having to waste an excessive amount of time explaining standard shared mathematical background, terminology, or notation--- or even worse, trying to explain the scientific method, the role of (simple! clearly defined!) thought experiments, or the neccessity of using mathematics and pictures to avoid ambiguities and facilitate qualitative conclusions as well as quantitative reasoning.
So why do I hate talking about these "paradoxes"? Because in the past I always seemed to wind up feeling that I was simply repeating for the n-th time stuff I or others have said dozens of times before:
Also, note that Wikipedia user pervect is also PF SA/M pervect, and Wikipedia user Mpatel is my former colleague in the now defunct "WikiProject Relativity", so I would expect versions of the Wikipedia articles which they edited to be much, much better than those rewritten by cranks. As for the current versions, that is anyone's guess. Note too that the old versions used old templates and figures which are in some cases no longer available, so their appearance has degraded.)
But my previous bad experiences trying to discuss these damnable "paradoxes" have occurred in "anything goes" fora like Wikipedia, or in regulated but public fora like the public areas of PF, where people with, shall we say, various levels of background and ability never hesitate to add their "two cents"--- almost invariably, with confidence inversely proportional to their understanding
Fortunately, the BRS is completely different from those venues: SA/Ms share some common background and experience and we can presume that SA/Ms don't enter discussions already convinced that "all the textbooks are wrong"--- an attitude encountered surprisingly awful in the roster of (often awful) arXiv eprints on these "paradoxes", much less public discussion forums or the Wikipedia. So this thread should hopefully be much more fun for me than any of my previous public discussions.
Since I have written extensively about these "paradoxes" many times before, let me briefly summarize in forthright language some lessons which I feel will be self-evident to anyone who has studied gtr at the graduate level and who has studied the most important contributions to the rather vast literature on "relativity paradoxes":
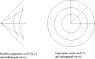
Speaking of pictures, DrGreg's figure in his Post #33 in
illustrates Bondi's concept of radar distance, which can be our default notion of "distance in the large" should any be needed. Fortunately, in Minkowski spacetime the null geodesics are explicitly known so computing radar distance exactly should be possible in simple physical scenarios.
Next, let me move straight into writing down two timelike congruences which are defined in certain regions of Minkowski spacetime, the Rindler and Bell congruences, and showing how to study them using their kinematic decomposition.
I hate talking about them! But I will force myself to try anyway.
What am I talking about? The so-called Bell spaceship "paradox" and Ehrenfest rotating disk "paradox". These paradoxes seem to come up every six to twelve months in PF, and always seem to lead to extremely long and thoroughly confused threads. As the discussion becomes increasingly heated and circular, the frequent result is that a Mentor locks the thread, and some of the disputants have even been banned from PF. These are not good outcomes.
Therefore, I think it will be useful to SA/Ms who regularly post in the relativity or astrophysics forums to have a place where we can show/discuss all the math and all the pictures without fear of interruption from possibly well intentioned newbies--- or even worse, from cranks. Without having to waste an excessive amount of time explaining standard shared mathematical background, terminology, or notation--- or even worse, trying to explain the scientific method, the role of (simple! clearly defined!) thought experiments, or the neccessity of using mathematics and pictures to avoid ambiguities and facilitate qualitative conclusions as well as quantitative reasoning.
So why do I hate talking about these "paradoxes"? Because in the past I always seemed to wind up feeling that I was simply repeating for the n-th time stuff I or others have said dozens of times before:
- in the Usenet Physics FAQ
Code:www.math.ucr.edu/home/baez/physics/Relativity/SR/rigid_disk.html - in Wikipedia articles
(notice that I have linked to the last version I edited of each article; I have nothing to do with subsequent versions, which might sometimes be better, but which may be more likely to be generally worse, given the number of cranks who want to have their say in Wikipedia),Code:en.wikipedia.org/w/index.php?title=Bell's_spaceship_paradox&oldid=57888610 en.wikipedia.org/w/index.php?title=Ehrenfest_paradox&oldid=58681705 en.wikipedia.org/w/index.php?title=Born_coordinates&oldid=53957524 en.wikipedia.org/w/index.php?title=Rindler_coordinates&oldid=51749949 en.wikipedia.org/w/index.php?title=Frame_fields_in_general_relativity&oldid=53048960 en.wikipedia.org/w/index.php?title=Congruence_(general_relativity)&oldid=49994474 - in PF posts:
Code:www.physicsforums.com/showpost.php?p=1524303&postcount=4 www.physicsforums.com/showthread.php?t=168121
Code:
gregegan.customer.netspace.net.au/SCIENCE/Rings/Rings.htmlBut my previous bad experiences trying to discuss these damnable "paradoxes" have occurred in "anything goes" fora like Wikipedia, or in regulated but public fora like the public areas of PF, where people with, shall we say, various levels of background and ability never hesitate to add their "two cents"--- almost invariably, with confidence inversely proportional to their understanding
Fortunately, the BRS is completely different from those venues: SA/Ms share some common background and experience and we can presume that SA/Ms don't enter discussions already convinced that "all the textbooks are wrong"--- an attitude encountered surprisingly awful in the roster of (often awful) arXiv eprints on these "paradoxes", much less public discussion forums or the Wikipedia. So this thread should hopefully be much more fun for me than any of my previous public discussions.
Since I have written extensively about these "paradoxes" many times before, let me briefly summarize in forthright language some lessons which I feel will be self-evident to anyone who has studied gtr at the graduate level and who has studied the most important contributions to the rather vast literature on "relativity paradoxes":
- The so-called Bell spaceship "paradox" is quite easily and conclusively settled by certain standard notions and techniques commonly encountered in the gtr literature:
- timelike congruences
- frame fields
- expansion and vorcitity tensor (from the kinematic decomposition of a timelike congruence)
- The expansion tensor, in particular, is precisely what is needed to decisively resolve the Bell "paradox"; people who insist upon excluding it will be forced to either reinvent special cases of the expansion tensor--- a notion which is very useful for almost everything in relativistic physics--- using private notation/terminology, or else will inevitably make mistakes and will very likely wind up "talking past" other disputants who are using their own private notation/terminology.
- The physics literature on "paradoxes", particularly in the past few decades, is full of really awful papers and arXiv eprints written by persons who
- don't know the literature on the subject even slightly,
- haven't even bothered to read such essential sources as the review article of Oyvind Gron, Am. J. Phys. 43 (1975): 869
- typically don't realize that they are trying to give a "not even wrong" "answer" [sic] to a question which was correctly answered by Langevin 1927 (in the more difficult case of the Ehrenfest paradox),
- rarely know about modern and obviously relevant techniques such as expansion and vorticity tensors,
- rarely know about the multiplicity of operationally significant notions of "distance in the large"--- that's a huge problem because this multiplicity is unavoidable even in flat spacetime, at least for accelerating observers, such as observers riding on a rigidly rotating disk, or Bell or Rindler observers riding on an alleged "taut cable",
- rarely understand the distinction between induced metrics on submanifolds (e.g. spatial hyperslices) and induced metrics on quotient manifolds (e.g. in the discussion of Landau and Lifschitz of the rotating disk),
- appear incapable of drawing a good sketch to clarify the physical scenarios they have in mind,
- insist upon using inadequate or inappropriate notation, terminology, and techniques.
Speaking of pictures, DrGreg's figure in his Post #33 in
Code:
www.physicsforums.com/showthread.php?t=428147&page=3Next, let me move straight into writing down two timelike congruences which are defined in certain regions of Minkowski spacetime, the Rindler and Bell congruences, and showing how to study them using their kinematic decomposition.
Last edited: