Can we solve this Morin's problem without conservation of string?

[ChiralSuperfields]

For this problem,

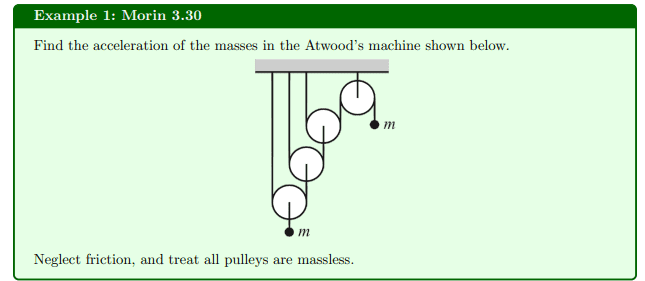
The solutions are,

However, how would we solve this without using the idea of conservation of string? Can we apply Newtons second law to each mass?

My working is:

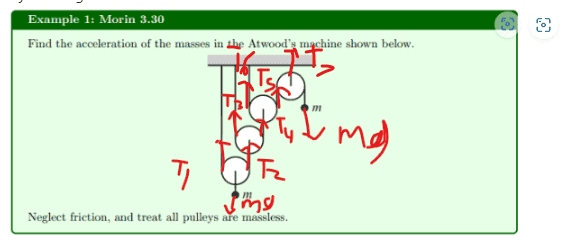
Then apply Newton's Second Law to each pulley,

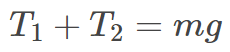(Line 1)

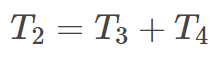(Line 2)

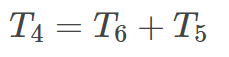(Line 3)

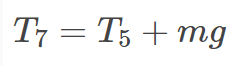(Line 4)
Many thanks!

 

[BiGyElLoWhAt]

I don't think your setup is quite right. Just looking at your first equation, you've set the tensions upward equal to gravity downward. This equation says they're equal, and the mass shouldn't move. You need an equation that gives it freedom to move. It should probably have an $a$ in it somewhere.
I don't ever remember using conservation of string to solve Atwoods problems. I could be misremembering, though.

 

[ChiralSuperfields]

I don't think your setup is quite right. Just looking at your first equation, you've set the tensions upward equal to gravity downward. This equation says they're equal, and the mass shouldn't move. You need an equation that gives it freedom to move. It should probably have an $a$ in it somewhere.
I don't ever remember using conservation of string to solve Atwoods problems. I could be misremembering, though.

Thank for your reply @BiGyElLoWhAt ! I will update that.

 

[Vanadium 50]

how would we solve this without using the idea of conservation of strin

If string isn't "conserved" (rather than created from nothing, maybe think of it being infinitely stretchable, like some sort oif idealized version of Silly Putty) the left three pullys will all fall to the floor. There's no tension in the strings because string length is not conserved, No solution.

 

[Lnewqban]

It seems to me that equation of line 4 is not correct.
T5, T6 and T7 must have the same value.

Can you visualize the system of pulleys as an instantaneous arrangement of levers?
If so, you could easily understand the relation of the external forces (mg left and mg right).

 

[ChiralSuperfields]

If string isn't "conserved" (rather than created from nothing, maybe think of it being infinitely stretchable, like some sort oif idealized version of Silly Putty) the left three pullys will all fall to the floor. There's no tension in the strings because string length is not conserved, No solution.

Thanks for your replies @Vanadium 50 and @Lnewqban ! Are you saying that the solution given by Kevin Zhou is incorrect? Many thanks!

 

[ChiralSuperfields]

(Line 1 fixed?)

(Line 4 fixed?)
Are the lines fixed now @Lnewqban ?

Many thanks,
Callum

 

[Vanadium 50]

"Correct" vs. "incorrect" isn't the way I would look at it. I would ask "are you solving the question asked"? When you remove the constant string length constraint, you allow the string to stretch, and with no constraint, your pulleys end up on the floor.

This means you don't want to give up that constraint.

 

[Lnewqban]

View attachment 318431(Line 1 fixed?)
View attachment 318432(Line 4 fixed?)
Are the lines fixed now @Lnewqban ?

Many thanks,
Callum

It seems that line 1 was correct as shown in post #1.
Without solving the whole problem, I would not know how correct lines 1 and 4 are as shown in post 7, sorry.

Why do you want to solve this without using the idea of conservation of string?

 

[BiGyElLoWhAt]

I think he's asking whether or not it's possible, meaning whether it's necessary to utilize that fact or not. I'm not sure that it is, now that I look at it more closely. Without actually solving it, I think you are going to end up with more unknowns than you have equations for.

As for equations 1 and 4, those look correct to me now, other than the fact that you have labeled your accelerations to be the same. You should give each mass it's own acceleration, or couple them together with another equation, probably involving the tensions.
I think the issue with trying to apply N2L here is that the pulleys are massless, they can't obey N2L, as any force would give rise to an infinite acceleration. You would need someway to work around the lack of mass, and effectively turn it into a kinematic equation, which I believe is one of the points of "conservation of string". Now you have equations dealing with distances (string lengths) as opposed to forces.

In general, if you have N variables, you should expect N equations to be able to get unique solutions, if they exist.

 

[ChiralSuperfields]

It seems that line 1 was correct as shown in post #1.
Without solving the whole problem, I would not know how correct lines 1 and 4 are as shown in post 7, sorry.

Why do you want to solve this without using the idea of conservation of string?

Thanks for your reply @Lnewqban , no worries! I want to solve this without conservation of string too see if it is possible to solve the problem with two methods.

Many thanks,
Callum

 

[Lnewqban]

Thanks for your reply @Lnewqban , no worries! I want to solve this without conservation of string too see if it is possible to solve the problem with two methods.

Many thanks,
Callum

You are welcome.
Try the system of imaginary levers described in post #4.

Locate the fulcrum of each lever at the point of each pulley that does not move for the imaginary very small period of time.
Then, for each pulley, you will have two more points to which forces are applied.
Note that you problem has three strings.

All pulleys look alike, but some serve only for changing the direction of the rope/cable/chain, while others act as levers, reducing the pulling effort in half and doubling the length of rope to pull.

 

[ChiralSuperfields]

I think he's asking whether or not it's possible, meaning whether it's necessary to utilize that fact or not. I'm not sure that it is, now that I look at it more closely. Without actually solving it, I think you are going to end up with more unknowns than you have equations for.

As for equations 1 and 4, those look correct to me now, other than the fact that you have labeled your accelerations to be the same. You should give each mass it's own acceleration, or couple them together with another equation, probably involving the tensions.
I think the issue with trying to apply N2L here is that the pulleys are massless, they can't obey N2L, as any force would give rise to an infinite acceleration. You would need someway to work around the lack of mass, and effectively turn it into a kinematic equation, which I believe is one of the points of "conservation of string". Now you have equations dealing with distances (string lengths) as opposed to forces.

In general, if you have N variables, you should expect N equations to be able to get unique solutions, if they exist.

Thank you @BiGyElLoWhAt , that was what I was trying to ask! Also thank you @Vanadium 50 for the stuff you said on string constraint! Also why would massless pulleys not obey Newton II?

According to this Physics SE post, Newton II is obeyed by massless pulleys [well at least the way I read it! :) ]

https://physics.stackexchange.com/q...m#:~:text=Yes it is OK to,if its mass is zero.

Many thanks,
Callum

 

[ChiralSuperfields]

You are welcome.
Try the system of imaginary levers described in post #4.

Locate the fulcrum of each lever at the point of each pulley that does not move for the imaginary very small period of time.
Then, for each pulley, you will have two more points to which forces are applied.
Note that you problem has three strings.

All pulleys look alike, but some serve only for changing the direction of the rope/cable/chain, while others act as levers, reducing the pulling effort in half and doubling the length of rope to pull.

Thanks again @Lnewqban - I will try the system of imaginary levers at some point!

Many thanks!