Cant get Venn diagram to agree with Demorgan's Law

[FrankJ777]

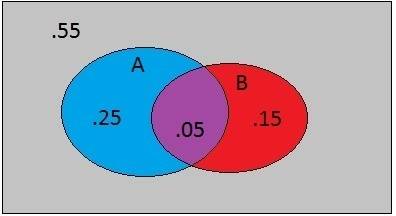
I was trying to solve a problem about calculating the probability of failures of a communications link with several nodes, and figured I need to use Demorgan's law since it would involve non mutually exclusive events. So I tried to go back to the basics to make sure I understand the axioms of probability and prove to my self that this is correct using Venn diagrams, but I can't make the numbers come out right trying to apply Demorgan's Law. Here is the example:

P(A) = .3
P(B) = .2

P(A∪B) = P(A) + P(B) - P(A∩B)
P(A∪B) = .3 + .2 - .05 = .45

But if I try to apply Demorgans's I don't get what I expect.

P(A∪B)' = P(A' ∩ B')
P(A∪B)' = (1-P(A))(1-P(B))
P(A∪B)' = (1-.3)(1-.2)
P(A∪B)' = (.7)(.8) = .56

but clearly P(A∪B)' = .55

so where am i going wrong? All parts of my Venn diagram add up to 1. Also I believe that the identity P(A∩B) = P(A)P(B) but this doesn't seem to be correct either as .3 x .2 ≠ .05. So I guess I'm misapplying the use of the Venn diagram but I'm not sure how. Can someone please explain what I'm doing wrong?

Thanks in advance.

 

[Erland]

P(A∪B)' = P(A' ∩ B')
P(A∪B)' = (1-P(A))(1-P(B))

The latter equality only holds if A and B are independent, i.e. if P(A ∩ B) = P(A)P(B) (which implies that also A' and B' are independent), but that is not the case here.

 

[BvU]

Where does the .05 come from, then ?

 

[stevendaryl]

But if I try to apply Demorgans's I don't get what I expect.

P(A∪B)' = P(A' ∩ B')
P(A∪B)' = (1-P(A))(1-P(B))
P(A∪B)' = (1-.3)(1-.2)
P(A∪B)' = (.7)(.8) = .56

Your second step is not correct. $P(A' \cap B')$ is only equal to $(1-P(A))(1-P(B))$ if $A$ and $B$ are mutually exclusive, that is, if $P(A \cap B) = 0$

 

[Erland]

Your second step is not correct. $P(A' \cap B')$ is only equal to $(1-P(A))(1-P(B))$ if $A$ and $B$ are mutually exclusive, that is, if $P(A \cap B) = 0$

Independent, not mutually exclusive. If we change P(A ∩ B) to 0.06, then the formula holds, but A and B are not mutually exclusive.

 

[stevendaryl]

Independent, not mutually exclusive. If we change P(A ∩ B) to 0.06, then the formula holds, but A and B are not mutually exclusive.

Right, my mistake.

 

[FrankJ777]

Ok. So can you only use Demorgan's for independent relations? If not I don't see how you can get P(A' ∩ B') if I can't use P(A' ∩ B') = (1 - P(A))(1-P(B)) .

 

[Stephen Tashi]

Ok. So can you only use Demorgan's for independent relations?

No, DeMorgan's laws aren't restricted to independent events.

If not I don't see how you can get P(A' ∩ B') if I can't use P(A' ∩ B') = (1 - P(A))(1-P(B)) .

The diagram can be partitioned into disjoint sets labeled according to whether they are in or not-in each of the named sets. This is like a coordinate system. So the distinct areas of the diagram have "coordinates" (A,B), (A,B'),(A',B), (A'B').

If you want the probability of the set $A'\cap B'$ (which corresponds to (A'B') ) take 1 minus the sum of the probabilities of the other sets in the partition. So $p(A'\cap B') = 1 - P(A'\cap B) - P(A\cap B') - P(A\cap B)$.

 

[FrankJ777]

Anyways I started this discussion because I was trying to figure out how to determine the probability of failure or success of a circuit, made of multiple links. Like this:
Node A-------link 1--------Node B---------link 2--------Node C
What is the chance a message getting to Node C from Node A if the chance of an individual link failing is .1?
Now, each link has an equal probability of failing.
Only one link needs to fail for the entire circuit to fail. But because multiple links could fail, their probabilities aren't mutually exclusive, so I can't just add the probabilities of the individual failures.
However since the failure of one link doesn't impact the probability that any other fails, they are independent meaning that the probability the probability of failure of link 1 and link 2 is P(f1 ∩ f2 ) = P(f1)P(f2)

So if i try to determine the probability of success of the circuit, that means both links must not fail, which is equivalent to P(f1 ∪ f2)' = P(f1' ∩ f2')
So the probability of success is:
P(f1 ∪ f2)' = P(f1' ∩ f2')
P(f1 ∪ f2)' = (1-P(f1))(1-P(f2))
P(f1 ∪ f2)' = (1-.1)(1-.1) = .9 x .9
P(f1 ∪ f2)' = . 81

Which agrees with my Venn diagram!

So I guess the key here was that the link failures are independent of each other and that's why I could use this technique.

Thanks a lot for the help guys. Hopefully I'll understand this better with some more practice.

 

[FrankJ777]

Oops. Correction on the Venn diagram.

 

[Erland]

Seems correct.