- #1
imsolost
- 18
- 1
This is my problem : it all starts with some very basic linear least-square to find a single parameter 'b' :
Y = b X + e
where X,Y are observations and 'e' is a mean-zero error term.
I use it, i find 'b', done.
But I need also to calculate uncertainties on 'b'. The so-called "model uncertainty" is needed and I've looked in the reference "https://link.springer.com/content/pdf/10.1007/978-1-4614-7138-7.pdf" where they define the "standard error" : SE(b) as :
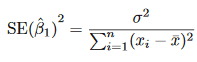
where sigma² = var(e).
So i have 'b' and var(b). Done.
Now here is the funny part :
I have mutliple sets of observations, coming from monte-carlo samplings on X and Y to account for analytical uncertaines on these observations. So basically, i can do the above stuff for each sample and i have like 1000 samples :
In the end, I have bi and [var(b)]i for i=1,...,1000.
Now the question : what is the mean and the standard deviation ?
What I've done :
1) i have looked in articles that do the same. i found this : "https://people.earth.yale.edu/sites/default/files/yang-li-etal-2018-montecarlo.pdf"
where (§2.3) they face the similar problem, they phrase it very well, but don't explain how they've done it...
2) Imagine you only account for analytical uncertainties. You would get 1000 values of 'b'. It would be easy to calculate a mean and a standard deviation with the common formulas for mean and sample variance. But here i don't have 1000 values ! I have 1000 random variables normally distributed following N(bi, SE(bi)).
3) i looked at multivariate normal distribution. When you have a list of random variables X1, X2,..., here is the expression for the mean and sample variance (basically what I'm looking for, i think) :
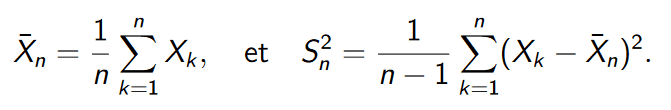
But i can't find how to calculate this if the X1, X2, ... are not iid (independant and identically distributed), because in my problem, they are independant but they are NOT identically distributed since N(bi, SE(bi)) is different for each 'i'.
4) For the mean it seems to be pretty straightforward and just be the mean of the bi. The standard deviation is the real problem to me.Please help :(
Y = b X + e
where X,Y are observations and 'e' is a mean-zero error term.
I use it, i find 'b', done.
But I need also to calculate uncertainties on 'b'. The so-called "model uncertainty" is needed and I've looked in the reference "https://link.springer.com/content/pdf/10.1007/978-1-4614-7138-7.pdf" where they define the "standard error" : SE(b) as :
where sigma² = var(e).
So i have 'b' and var(b). Done.
Now here is the funny part :
I have mutliple sets of observations, coming from monte-carlo samplings on X and Y to account for analytical uncertaines on these observations. So basically, i can do the above stuff for each sample and i have like 1000 samples :
In the end, I have bi and [var(b)]i for i=1,...,1000.
Now the question : what is the mean and the standard deviation ?
What I've done :
1) i have looked in articles that do the same. i found this : "https://people.earth.yale.edu/sites/default/files/yang-li-etal-2018-montecarlo.pdf"
where (§2.3) they face the similar problem, they phrase it very well, but don't explain how they've done it...
2) Imagine you only account for analytical uncertainties. You would get 1000 values of 'b'. It would be easy to calculate a mean and a standard deviation with the common formulas for mean and sample variance. But here i don't have 1000 values ! I have 1000 random variables normally distributed following N(bi, SE(bi)).
3) i looked at multivariate normal distribution. When you have a list of random variables X1, X2,..., here is the expression for the mean and sample variance (basically what I'm looking for, i think) :
But i can't find how to calculate this if the X1, X2, ... are not iid (independant and identically distributed), because in my problem, they are independant but they are NOT identically distributed since N(bi, SE(bi)) is different for each 'i'.
4) For the mean it seems to be pretty straightforward and just be the mean of the bi. The standard deviation is the real problem to me.Please help :(