Conditional probability reasoning problem

[diredragon]

Homework Statement

Out of all the products a company makes 2% is damaged. During the routine control of the products, the products are put to a test which discovers the damaged ones in 99% of the cases. In 1% however it approves the damaged item as a working one and vice versa. Find the probability that the product is working under the condition that it was disapproved by the test and the probability of the product which is damaged but under the condition that it was approved by the test.
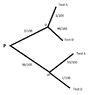
See the image below:

Test A = Test Approved
Test B = Test Disapproved

Homework Equations

3. The Attempt at a Solution [/B]
The solution to this problem comes rather un-intuitively to me.
I am looking for $P(W/T_D)$ (working under the condition that it is disapproved) and
$P(D/T_A)$ (damaged under the condition that it is approved).
The textbook solution does so in this way:
$P(D) = 2/100$
$P(W) = 98/100$
$P(T_D/D) = 99/100$ (test disapproved under the condition that its damaged)
$P(T_A/D) = 1/100$
$P(T_D/W) = 1/100$
$P(T_A/W) = 99/100$
They used the Bayes theorem here stating:
$P(W/T_D) = \frac{P(T_D/W)P(W)}{P(T_D)} = \frac{P(T_D/W)P(W)}{P(T_D/W)P(W) + P(T_D/D)P(D)} = 0.33$ which which I am not sure what says. That 33% of the working products get thrown away?
Much reasonable seems a simple answer as:
$\frac{98}{100}*\frac{1/100} = 0.0098$ which would tell us that out of all the products the working discarder ones are a small fraction rather than a massive 33%.
What am i missing? Am i not understanding the question because the order of which it says by the condition must make some difference but i don't see it.

 

[Orodruin]

That 33% of the working products get thrown away?

No, that would be $P(T_D|W)$, i.e., the probability to throw away the product if it is working. What you have is $P(W|T_D)$, the probability that a thrown away product is actually working. Those are different probabilities.

 

[diredragon]

No, that would be $P(T_D|W)$, i.e., the probability to throw away the product if it is working. What you have is $P(W|T_D)$, the probability that a thrown away product is actually working. Those are different probabilities.

Right, so $P(T_D|W)$ being the probability that the product will be thrown away if it is working is small $1/100$ because that's how the test was created. On the other side $P(W|T_D)$ is the probability of the thrown away product working meaning all I'm observing is a bunch of thrown away products and since the working products made are much more present than the damaged ones in the manufacturing even though the test is rigorous they will make a significant percent of the thrown away products because of the vast differences in working/damaged products made in the start. Did i get this right?

 

[Orodruin]

Yes, it tells you that a third of the thrown products are actually working. But the number of thrown away products is not that large.

 

[diredragon]

Yes, it tells you that a third of the thrown products are actually working. But the number of thrown away products is not that large.

Amazing! Thanks