Conservation of Mass for Compressible Flow

[erobz]

I'm trying to figure out how the mathematics of conservation of mass in compressible flow works for a simple setup. I posted this problem in hw physics section, and the conversation turned to the physics model and appears to have gone kaput. This was supposed to be a mathematics question (but its difficult to untangle completely from the physics), so it went to the wrong forum.

In the top position the system is static. The mass of air in the pipe at $t=0$ is $M_i$, then the piston starts to advance pushing air out of the outlet $o$. The density $\rho$ of the flow across the remainder of the tube will vary in the coordinate $u$, and time $t$. the origin of $u$ is to ride along with the piston and will always range from $0 \leq u \leq l-x(t)$.

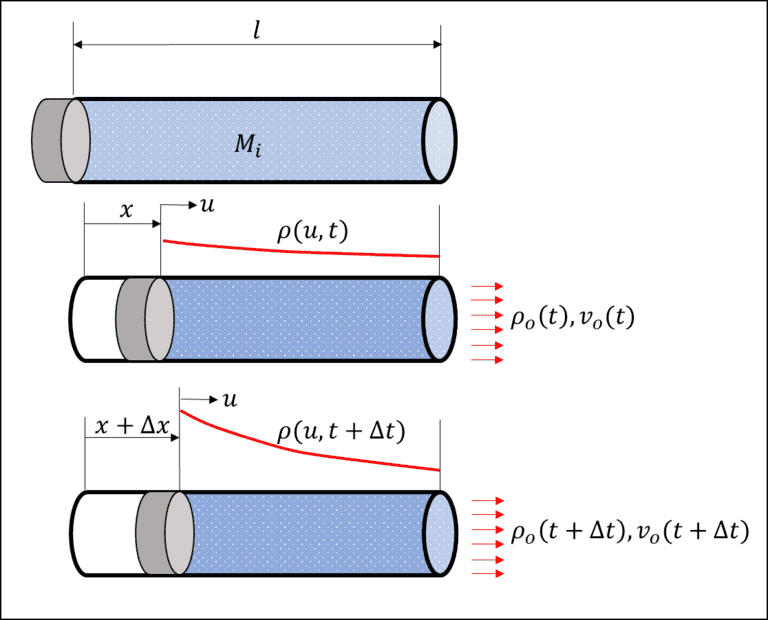The properties ( density and velocity) are distributed uniformly across any particular section ( I'm ignoring realities of what the flow properties look like in transverse directions)

With the subscript $o$ referring to the properties at the fixed location of the outlet. At any fixed time $t$ to get the mass inside the control volume I get that:

$$ M_{cv} = \int_0^{u(t)} A~ \rho (u,t)~du $$

Also, at any time $t$ the rate of change of mass in the control volume is:

$$ \frac{d}{dt}M_{cv} = - A \rho_o(t) v_o(t) $$

So it seems (to me) like I can combine those two equations:

$$ \frac{d}{dt} \left( \int_0^{u(t)} A~ \rho (u,t) ~du \right) = - A \rho_o(t) v_o(t) $$

Now, $u(t)$ ( the upper limit of integration on the LHS) at any fixed time $t$ can be found from the position of the piston w.r.t. to origin:

$$ u(t) = l- x(t) = l - \int_0^t \dot x ~dt $$

My question is:

If I haven't already committed mathematical heresy, is there any way to get $\rho (u,t)$ as a function of all the other variables? It seems like the variable of $u$ is trapped in the integral in some kind of partial integration ( I'm out of my depth on the proper nomenclature), because the variable of the integration is not itself a function of time, just the upper limit. I'm all twisted up on this...

Thanks for any help untangling this mess I'm making.

 

[Frabjous]

What in your equation prevents all of the gas from moving instantaneously to the end of the barrel and then leaking out slowly at v₀(t)?

To keep things simple, you have two unknown functions ρ(u,t) and v(u,t) and one equation so you do not have enough information to solve. All that physics stuff you want to ignore from your previous post is how one goes about remedying the situation.

 

[erobz]

What in your equation prevents all of the gas from moving instantaneously to the end of the barrel and then leaking out slowly at v₀(t)?

Conservation of mass can be applied independently. I demand that there will be a distribution of density along the tube with the mathematics, the forces that make said distributions are irrelevant to conservation of mass in the system. Mass conservation is more fundamental that Newtons Laws. I'm trying to understand the motivation for partial differential equations here. Not the forces.

 

[Frabjous]

Conservation of mass can be applied independently. I demand that there will be a distribution of density along the tube with the mathematics, the forces that make said distributions are irrelevant to conservation of mass in the system.

No. To determine the velocity of the flow at the end of the barrel you need conservation of momentum which means that you need a pressure variable. You also need to define your material so you will need an equation of state.

 

[erobz]

No. To determine the velocity of the flow at the end of the barrel you need conservation of momentum which means that you need a pressure variable. You also need to define your material so you will need an equation of state.

I shouldn't have to determine the velocity of the flow at the end at this point. I'm only applying conservation of mass. All I need to know is that the properties at the outlet will be some pure function of time $t$, same goes for the density of the gas at the end. If we can't find $\rho(u,t)$,so be it. My interest is only in applying the math, I don't want to derail it again with the next steps in the physics model which defines all these functions.

It really is just about uncovering the motivation for the differential form of the continuity equation as some natural extension of what I'm doing:

$$ \frac{\partial \rho}{\partial t} + \nabla ( \rho \boldsymbol v) = 0 $$

Maybe its not there, maybe it is.

 

[Frabjous]

I demand that there will be a distribution of density along the tube

Your demand is not reflected in your equations, so things are not solvable as is.

 

[erobz]

Your demand is not reflected in your equations, so things are not solvable as is.

Fine,...forget about solving for $\rho(u,t)$. I'm trying to see how the differential form of the continuity arises. It's seems reasonably close to what I'm saying, I just can't make the connection in the mathematics.

 

[Frabjous]

What equation do you not understand?

 

[erobz]

What equation do you not understand?

It really is just about uncovering the motivation for the differential form of the continuity equation as some natural extension of what I'm doing:

$$ \frac{\partial \rho}{\partial t} + \nabla ( \rho \boldsymbol v) = 0 $$

Maybe its not there, maybe it is.

 

[Frabjous]

It should be divergence, not gradient.
The basic idea is that material flows in/out of a control volume with a mass flux. If the mass flux is not spatially constant, net material can be deposited/removed to/from the control volume changing the density.
What exactly do you not understand about the derivation?

 

[erobz]

I keep getting to these points where it seems like if you don't know how to explain everything, you suddenly know nothing. This problem seems like it should be pretty straight forward, but alas...

It should be divergence, not gradient.

In my fluids text its the "del" operator. It looks like the gradient to me because they define:

$$ \nabla = \mathbf{i} \frac{\partial}{\partial x } + \mathbf{j} \frac{\partial}{\partial y } + \mathbf{k} \frac{\partial}{\partial z} $$

I don't even know what the divergence is.

The basic idea is that material flows in/out of a control volume with a mass flux. If the mass flux is not constant, net material can be deposited/removed from the control volume changing the density.
What exactly do you not understand about the derivation?

I understand the basic idea ( I think ) but it seems tantalizingly close to what I'm trying to do in the OP, do you not agree? I just can't make the connection. Maybe it looks nothing like it to the trained eye, and I'm just deluded.

 

[Frabjous]

Divergence is when you take the dot product with del.
The issue with your construction is that you are not taking the limit of zero volume and that the two sides of the volume are “different”
Most engineering proofs take a first order taylor expansion of the mass flux on either side of the box and subtract.

 

[erobz]

Divergence is when you take the dot product with del.

Yeah, I see that they have taken the dot product. Are there different symbols? del and divergence look identical to me...

EDIT: nevermind I think you mean i shoud have written:

$$ \frac{\partial \rho}{\partial t} + \nabla \cdot ( \rho \boldsymbol v) = 0 $$

The issue with your construction is that you are not taking the limit of zero volume and that the two sides of the volume are “different”
Most engineering proofs take a first order taylor expansion of the mass flux on either side of the box and subtract.

I can see that as an issue. My control volume is not a point, I was hoping the distributions would take care of that after differentiating my result somehow. Perhaps that is a fools errand.

 

[Frabjous]

Here’s a quick derivation for a unit volume $\Delta x \Delta y \Delta z$ for flow u in the x-direction
m_subscript are per unit time. I am doing a first-order Taylor expansion around the center of the box
$\dot m = m_{in}-m_{out}$
$\frac {\partial \rho} {\partial t}\Delta x \Delta y \Delta z= (\rho u+\frac {\partial (\rho u)} {\partial x}\frac {-\Delta x} 2)\Delta y \Delta z -( \rho u + \frac {\partial (\rho u)} {\partial x}\frac {\Delta x} 2))\Delta y \Delta z$
$\frac {\partial \rho} {\partial t}\Delta x = (\rho u+\frac {\partial (\rho u)} {\partial x}\frac {-\Delta x} 2) -(\rho u + \frac {\partial (\rho u)} {\partial x}\frac {\Delta x} 2)$
$\frac {\partial \rho} {\partial t}\Delta x = - \frac {\partial (\rho u)} {\partial x}\Delta x$
$0=\frac {\partial \rho} {\partial t}+\frac {\partial (\rho u)} {\partial x}$

 

[Frabjous]

You can also take my first equation and then do the integral formulation. You can then use the divergence theorem to change the surface integral to a volume integral.

 

[erobz]

Here’s a quick derivation for a unit volume $\Delta x \Delta y \Delta z$ for flow u in the x-direction
m_subscript are per unit time. I am doing a first-order Taylor expansion around the center of the box
$\dot m = m_{in}-m_{out}$
$\frac {\partial \rho} {\partial t}\Delta x \Delta y \Delta z= (\rho u+\frac {\partial (\rho u)} {\partial x}\frac {-\Delta x} 2)\Delta y \Delta z -( \rho u + \frac {\partial (\rho u)} {\partial x}\frac {\Delta x} 2))\Delta y \Delta z$
$\frac {\partial \rho} {\partial t}\Delta x = (\rho u+\frac {\partial (\rho u)} {\partial x}\frac {-\Delta x} 2) -(\rho u + \frac {\partial (\rho u)} {\partial x}\frac {\Delta x} 2)$
$\frac {\partial \rho} {\partial t}\Delta x = - \frac {\partial (\rho u)} {\partial x}\Delta x$
$0=\frac {\partial \rho} {\partial t}+\frac {\partial (\rho u)} {\partial x}$

Why should we expand about the center of the element, as opposed to either face? My textbook makes it a point to do this also, but it doesn't seem to be mathematically necessary?

 

[Frabjous]

Why should we expand about the center of the element, as opposed to either face? My textbook makes it a point to do this also, but it doesn't seem to be mathematically necessary?

Those are subtleties I have long forgotten. I did it because I wanted $\frac {\partial \rho} {\partial t}$ in the center. Since I am using the zeroth order Taylor expansion for it, I agree that it doesn’t seem to matter. I’ll check a couple of books tomorrow to see if they say anything.

 

[Frabjous]

While not answering your question, I noticed that $-(\rho u|_x -\rho u|_{x+\Delta x})/\Delta x$ is the definition of the derivative without the Taylor expansion stuff. I will still look for info about left, center or right definitions.

 

[Frabjous]

While not answering your question, I noticed that $-(\rho u|_x -\rho u|_{x+\Delta x})/\Delta x$ is the definition of the derivative without the Taylor expansion stuff. I will still look for info about left, center or right definitions.

I couldn‘t find a good discussion on the topic. I don’t think any of the approaches is incorrect in the limit; however this can matter when looking at the discrete limit (i.e., numerical analysis).

I think the least arguable way is the approach I described in post 15.

 

[erobz]

So I gather that to actually solve this problem we are going to be working with the Navier Stokes equations.

 

[Frabjous]

So I gather that to actually solve this problem we are going to be working with the Navier Stokes equations.

It depends on what specifically you are trying to do. For compressible flow, you generaly start with the conservation equations with an equation of state. There are simplifications if you are dealing with shocks or are in the acoustic limit.

 

[erobz]

It depends on what specifically you are trying to do. For compressible flow, you generaly start with the conservation equations with an equation of state. There are simplifications if you are dealing with shocks or are in the acoustic limit.

I would have liked to find the pressure acting on the front of the piston as it pushes the air out of the tube in-terms of the acceleration of the piston. I didn’t want to consider effects the shockwave as the tube is short. I would like to account for viscous effects in some simplified way. However, I don’t think viscous effects are required to set up a pressure gradient along the tube so long as the piston is accelerating, so I’d just ignore that for now. Basically I was hoping for a model just a touch better than “it’s atmospheric pressure ahead of the piston”.

 

[Frabjous]

I would have liked to find the pressure acting on the front of the piston as it pushes the air out of the tube in-terms of the acceleration of the piston. I didn’t want to consider effects the shockwave as the tube is short. I would like to account for viscous effects in some simplified way. However, I don’t think viscous effects are required to set up a pressure gradient along the tube so long as the piston is accelerating, so I’d just ignore that for now. Basically I was hoping for a model just a touch better than “it’s atmospheric pressure ahead of the piston”.

I would start a new thread.

A couple of thoughts.
For most guns the pressure behind the projectile would be significantly higher than atmospheric pressure. You should check your system.
I would suggest using the method of characteristics. One you figure out the equations for a single velocity jump, the rest is just repeating things in a spread sheet.
You might find this of help. https://www.nasa.gov/sites/default/...ables-Charts-CompressibleFlow-Report-1135.pdf

 

[erobz]

I would start a new thread.

It’s just unfinished business from this thread:

https://www.physicsforums.com/threads/optimization-of-barrel-length-in-pneumatic-cannons.1053420/

 

[vanhees71]

I don't know, which level of rigor you need. The physics derivation is as follows. Consider a fluid described by the flow field $\vec{v}(t,\vec{x})$ and a mass density $\rho(t,\vec{x})$. Now consider a volume $V$ with boundary $\partial V$ with the surface-normal vectors pointing outwards (that's the standard convention used in physics) at rest. Then the conservation of mass (valid in Newtonian physics) says that the change of the mass contained in the volumen,
$$M_V(t)=\int_{V} \mathrm{d}^3 x \rho(t,\vec{x})$$
is due to fluid moving in or out of the volume through the surface. In a time increment $\mathrm{d} t$ the amount of mass flowing through a surface elemente $\mathrm{d}^2 \vec{f}$ is $\mathrm{d} m=\mathrm{d}^2 \vec{f} \cdot \mathrm{d} t \rho(t,\vec{x}) \vec{v}(t,\vec{x})$. Applying this to the boundary surface $\partial V$ you have to count this negative, because $\mathrm{d} m>0$ means that this amount of mass flows out of the volume. Thus you have
$$\mathrm{d} m = \mathrm{d} t \dot{M}_V(t) = \mathrm{d} t \int_V \mathrm{d}^3 x \partial_t \rho(t,\vec{x}) = -\mathrm{d} t \int_{\partial V} \mathrm{d}^2 \vec{f} \cdot \rho(t,\vec{x}) \vec{v}(t,\vec{x}).$$
dividing by $\mathrm{d} t$ gives
$$\int_V \mathrm{d}^3 x \partial_t \rho(t,\vec{x})=-\int_{\partial V} \mathrm{d}^2 \vec{f} \cdot \rho(t,\vec{x}) \vec{v}(t,\vec{x}).$$
Using Gauss's integral theorem, you can write the surface integral as a volume integral over the divergence of the integrated vector field,
$$\int_V \mathrm{d}^3 x \partial_t \rho(t,\vec{x})=-\int_V \mathrm{d}^3 x \vec{\nabla} \cdot [\rho(t,\vec{x}) \vec{v}(t,\vec{x})].$$
Since this holds for any volume $V$, you can make it as small as you like around a point $\vec{x}$, and this finally leads to the local version of the mass-conservation law, the continuity equation
$$\partial_t \rho(t,\vec{x}) + \vec{\nabla} \cdot \vec{j}(t,\vec{x})=0$$
with the mass-current density,
$$\vec{j}(t,\vec{x})=\rho(t,\vec{x}) \vec{v}(t,\vec{x}).$$

 

[erobz]

I don't know, which level of rigor you need. The physics derivation is as follows. Consider a fluid described by the flow field $\vec{v}(t,\vec{x})$ and a mass density $\rho(t,\vec{x})$. Now consider a volume $V$ with boundary $\partial V$ with the surface-normal vectors pointing outwards (that's the standard convention used in physics) at rest. Then the conservation of mass (valid in Newtonian physics) says that the change of the mass contained in the volumen,
$$M_V(t)=\int_{V} \mathrm{d}^3 x \rho(t,\vec{x})$$
is due to fluid moving in or out of the volume through the surface. In a time increment $\mathrm{d} t$ the amount of mass flowing through a surface elemente $\mathrm{d}^2 \vec{f}$ is $\mathrm{d} m=\mathrm{d}^2 \vec{f} \cdot \mathrm{d} t \rho(t,\vec{x}) \vec{v}(t,\vec{x})$. Applying this to the boundary surface $\partial V$ you have to count this negative, because $\mathrm{d} m>0$ means that this amount of mass flows out of the volume. Thus you have
$$\mathrm{d} m = \mathrm{d} t \dot{M}_V(t) = \mathrm{d} t \int_V \mathrm{d}^3 x \partial_t \rho(t,\vec{x}) = -\mathrm{d} t \int_{\partial V} \mathrm{d}^2 \vec{f} \cdot \rho(t,\vec{x}) \vec{v}(t,\vec{x}).$$
dividing by $\mathrm{d} t$ gives
$$\int_V \mathrm{d}^3 x \partial_t \rho(t,\vec{x})=-\int_{\partial V} \mathrm{d}^2 \vec{f} \cdot \rho(t,\vec{x}) \vec{v}(t,\vec{x}).$$

Notation is certainly more fancy than I'm used to, but I think I basically follow it up to here.

Using Gauss's integral theorem, you can write the surface integral as a volume integral over the divergence of the integrated vector field,
$$\int_V \mathrm{d}^3 x \partial_t \rho(t,\vec{x})=-\int_V \mathrm{d}^3 x \vec{\nabla} \cdot [\rho(t,\vec{x}) \vec{v}(t,\vec{x})].$$

This is probably going to take me significant study to unpack. Gauss's integral theorem, divergence ect...is new to me yesterday when @Frabjous mentioned it.

But thank you for sharing.

 

[Frabjous]

The gaps you have identified are usually addressed in a vector calculus course.

 

[erobz]

Yeah, I still have my Calculus textbook. The topics are covered over a few of the last chapters in it, I don't think we covered the more advanced 3D concepts in the Calc 3 course.

 

[wrobel]

Let $\omega$ be a k-form on m-dimensional manifold $M,\quad m\ge k.$ Let $v$ be a vector field on $M$ and $g^t$ be its flow.

Let $S\subset M$ be a k-dimensional compact submanifold. Then
$$\frac{d}{dt}\Big|_{t=0}\int_{g^t(S)}\omega=\int_SL_v\omega.$$ Here $L_v$ is a Lie derivative and the formula follows directly from the change of variables.

Particularly if k=m then $\omega=\rho(x)dx^1\wedge\ldots\wedge dx^m$ and
$$L_v\omega=\frac{\partial (\rho v^i)}{\partial x^i} dx^1\wedge\ldots\wedge dx^m.$$

From the group property it is not hard to show that the following conditions are equivalent

1) $\frac{d}{dt}\Big|_{t=0}\int_{g^t(S)}\omega=0$ for any k-dimensional compact submanifold S;
2) $\frac{d}{dt}\int_{g^t(S)}\omega=0,\quad \forall t$ and for any k-dimensional compact submanifold S;
3) $L_v\omega=0$

This method is covering a lot of different circulations theorems in electrodynamics and hydro dynamics as well

 

[erobz]

Let $\omega$ be a k-form on m-dimensional manifold $M,\quad m\ge k.$ Let $v$ be a vector field on $M$ and $g^t$ be its flow.

Let $S\subset M$ be a k-dimensional compact submanifold. Then
$$\frac{d}{dt}\Big|_{t=0}\int_{g^t(S)}\omega=\int_SL_v\omega.$$ Here $L_v$ is a Lie derivative and the formula follows directly from the change of variables.

Particularly if k=m then $\omega=\rho(x)dx^1\wedge\ldots\wedge dx^m$ and
$$L_v\omega=\frac{\partial (\rho v^i)}{\partial x^i} dx^1\wedge\ldots\wedge dx^m.$$

From the group property it is not hard to show that the following conditions are equivalent

1) $\frac{d}{dt}\Big|_{t=0}\int_{g^t(S)}\omega=0$ for any k-dimensional compact submanifold S;
2) $\frac{d}{dt}\int_{g^t(S)}\omega=0,\quad \forall t$;
3) $L_v\omega=0$

Thank you for the reply, however I’m just smart enough to realize I’m completely in the dark with this level of analysis.

 

[vanhees71]

Let $\omega$ be a k-form on m-dimensional manifold $M,\quad m\ge k.$ Let $v$ be a vector field on $M$ and $g^t$ be its flow.

Let $S\subset M$ be a k-dimensional compact submanifold. Then
$$\frac{d}{dt}\Big|_{t=0}\int_{g^t(S)}\omega=\int_SL_v\omega.$$ Here $L_v$ is a Lie derivative and the formula follows directly from the change of variables.

Particularly if k=m then $\omega=\rho(x)dx^1\wedge\ldots\wedge dx^m$ and
$$L_v\omega=\frac{\partial (\rho v^i)}{\partial x^i} dx^1\wedge\ldots\wedge dx^m.$$

From the group property it is not hard to show that the following conditions are equivalent

1) $\frac{d}{dt}\Big|_{t=0}\int_{g^t(S)}\omega=0$ for any k-dimensional compact submanifold S;
2) $\frac{d}{dt}\int_{g^t(S)}\omega=0,\quad \forall t$ and for any k-dimensional compact submanifold S;
3) $L_v\omega=0$

This method is covering a lot of different circulations theorems in electrodynamics and hydro dynamics as well

In the fluid-mechanics literature those are known also as "Reynolds transport theorems". This is the modern Cartan-calculus formulation of them.

 

[wrobel]

Yes! Elie Cartan's integral invariants.

Df. A form $\omega$ is called relative integral invariant iff $L_v\omega=d\Omega\quad (\exists \Omega)$.
A form $\alpha$ is called absolute integral invariant iff $L_v\alpha=0$.

If $\omega$ is a relative integral invariant then $d\omega$ is an absolute integral invariant: $L_vd\omega=dL_v\omega=dd\Omega$
and
$$\frac{d}{dt}\Big|_{t=0}\int_{g^t(S)}\omega=\int_SL_v\omega=\int_{\partial S}\Omega.$$

For further play with these formulas use
$$L_v\omega=i_vd\omega+di_v\omega;$$

De Rham's theorem is also near here
etc.

For example in the extended phase space of a Hamiltonian system one has: $dp_i\wedge dx^i-dH\wedge dt$ is an absolute integral invariant; $p_idx^i-Hdt$ is a relative integral invariant.

 

[erobz]

In the fluid-mechanics literature those are known also as "Reynolds transport theorems". This is the modern Cartan-calculus formulation of them.

The funny thing is, I know about Reynolds Transport Theorems, but I never would have recognized that(and frankly still can’t)! @wrobel said “k form on m dimensional manifold” and my head exploded.

 

[vanhees71]

The advantage of the modern Cartan calculus is that it becomes in a way very natural, and it's very general too, because it works not only in (pseudo)-Riemannian manifolds but in general differentiable manifolds, i.e., the Lie derivative and Stokes's theorem for alternating (differential) forms are independent of any additional structures like connections and/or (pseudo-)metrics.