- #1
jarekduda
- 82
- 5
In NP problems we can cheaply (polynomial time) test if a given input is satisfying, but the difficulty is that there is an exponential number of possible inputs - the question is if e.g. there is a satisfying input.
Imagine there is a simple hardware implementation of verifier (e.g. in form of 3-SAT problem): as a few layers of logic gates, returns 1 if the input is satisfying, 0 otherwise.
Now build a circuit which returns "input+1" (cyclically) for non-satifying inputs, and "input" for a satisfying one ... and connect its output to input:
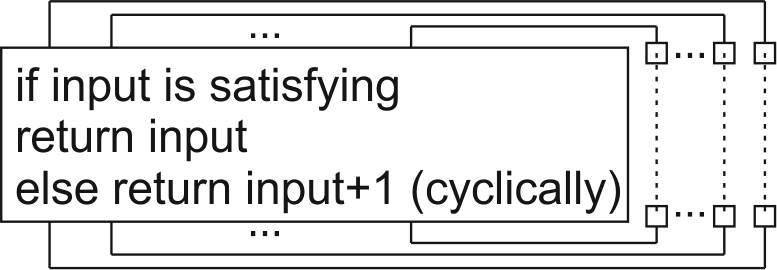
So the original NP problem has became finding a fixed-point of such loop. If this electronic circuit has a clock (is synchronized), it would test one input per step, until reaching a fixed point - a solution.
But what if there is no clock/synchronization? Just hydrodynamics of electrons flowing around the circuit, trying to stabilize the flow to minimize fluctuations. Like NOT gate connected into a loop should create oscillation (I think it strongly depends on technology of gates?).
Could such unsynchronized continuous circuit be faster - use some shortcuts while searching for the fixed point of the loop: solution of our problem?
While we know that with clock it stabilizes in exponential time, without the clock there are basically 3 options:
Can we say anything certain without experiment (ASIC?) - are there any concrete arguments pro or against any of these possibilities?
I have tried asking it on stackexchange, where Peter Shor has commented, but still there are no concrete arguments.
Imagine there is a simple hardware implementation of verifier (e.g. in form of 3-SAT problem): as a few layers of logic gates, returns 1 if the input is satisfying, 0 otherwise.
Now build a circuit which returns "input+1" (cyclically) for non-satifying inputs, and "input" for a satisfying one ... and connect its output to input:
So the original NP problem has became finding a fixed-point of such loop. If this electronic circuit has a clock (is synchronized), it would test one input per step, until reaching a fixed point - a solution.
But what if there is no clock/synchronization? Just hydrodynamics of electrons flowing around the circuit, trying to stabilize the flow to minimize fluctuations. Like NOT gate connected into a loop should create oscillation (I think it strongly depends on technology of gates?).
Could such unsynchronized continuous circuit be faster - use some shortcuts while searching for the fixed point of the loop: solution of our problem?
While we know that with clock it stabilizes in exponential time, without the clock there are basically 3 options:
- Without clock it will no longer stabilize,
- It will stabilize in comparable time,
- It will stabilize essentially faster (using some shortcuts of the continuous search).
Can we say anything certain without experiment (ASIC?) - are there any concrete arguments pro or against any of these possibilities?
I have tried asking it on stackexchange, where Peter Shor has commented, but still there are no concrete arguments.