Crosswind problem (pgs. 34-35, Thinking Physics, 3rd edition)

[A.T.]

So what is the hypothesis for the limits of $v_x,v_y$?

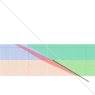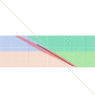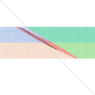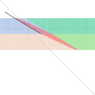
Here the speed limits plotted as function of the minimal apparent wind angle (AWA), normalized to multiples of true wind speed (TWS):

And here the speeds for AWA = 6° (ice boats) and AWA = 20° (racing boats), as function of the true wind angle (TWA), or the course relative to the true wind:

For the AWA = 20°, here the vectors for maximal speed:

Maximal downwind component:

Maximal upwind component:

The math:

LD_air = lift/drag at the air
LD_surface = lift/drag at the surface

AWA : apparent wind angle
TWA : true wind angle
TWS : true wind speed

AWA = atan(1 / LD_surface) + atan(1 / LD_air)

MAX_SPEED = TWS * 1 / sin(AWA)
MAX_DOWNWIND_COMPONENT = TWS * (1 / sin(AWA) + 1) / 2
MAX_UPWIND_COMPONENT = TWS * (1 / sin(AWA) - 1) / 2

SPEED = TWS * sin(TWA - AWA) / sin(AWA)
DOWNWIND (+) UPWIND (-) COMPONENT= - SPEED * COS(TWA)

For more information see:
http://www.onemetre.net/design/CourseTheorem/CourseTheorem.htm
https://books.google.de/books?id=Xe_i23UL4sAC&lpg=PP1&hl=de&pg=PA49#v=onepage&q&f=false

 

[erobz]

I believe you’ve already posted this, I didn’t understand it then, and I don’t now. The links have almost no supporting analysis. Surely someone has completed a full analysis?

 

[A.T.]

I believe you’ve already posted this, I didn’t understand it then, and I don’t now.

It's just basic geometry. Are you familiar with inscribed angles?
https://en.wikipedia.org/wiki/Inscribed_angle

The apparent wind angle (AWA) is the inscribed angle and determines the size of the polar circle, which constrains the velocity vector. The greater the lift/drag ratios, the smaller the AWA, and the larger the circle of possible velocities.

Just play around with this interactive diagram, move the sliders around and try different situations:
https://www.geogebra.org/m/tj5qf3w2

 

[A.T.]

What have I goofed on already?

As I explained in post #247, using a 1D jet for the 2D case doesn't make much sense.

Here is an animation to visualize the kinematics with respect to the 2D air-mass, rather than a single jet.

The relative flow is along the bottom/left or top/right edge of the red area. And relative to the flow we have empirical data on lift(L)/drag(D) we can achieve. Shown below is a conservative L/D=8 which still results in the aerodynamics force (F) having a positive component along the direction of motion (P).

 

[erobz]

Here is an animation to visualize the kinematics with respect to the 2D air-mass, rather than a single jet.

View attachment 333400

The relative flow is along the bottom/left or top/right edge of the red area. And relative to the flow we have empirical data on lift(L)/drag(D) we can achieve. Shown below is a conservative L/D=8 which still results in the aerodynamics force (F) having a positive component along the direction of motion (P).

View attachment 333399

My interest was theoretical (I can't even say I have interest anymore - this was started almost a year ago). If you are insistent in dragging us back in, I would like to see a "Newtons 2nd Law" approach, or figure out how to model it myself using Newton 2nd Law. I'm not really interested in further discussion unless its analytical. If the result is empirical(as you say), then there must be some set of stepping stone models to get to the empirical evidence.

 

[A.T.]

My interest was theoretical (I can't even say I have interest anymore - this was started almost a year ago). If you are insistent in dragging us back in, I would like to see a "Newtons 2nd Law" approach, or figure out how to model it myself using Newton 2nd Law. I'm not really interested in further discussion unless its analytical. If the result is empirical(as you say), then there must be some set of stepping stone models to get to the empirical evidence.

If you are interested in finding a theoretical limit on the ratio between a boat's downwind velocity component and windspeed, then that is doomed to fail, as there is no theoretical limit on mechanical advantage / gear ratio. All limits here are practical and stem from our limitations in achieving higher efficiency while preserving sufficient structural stability. For airfoils / hydrofoils those efficiencies are expressed as lift/drag ratios, and lead to velocity limits via the course theorem as explained in post #281. Those lift/drag ratios can be derived empirically or numerically (CFD).

If you are interested in a purely analytical derivation from Newton 2nd Law, then you have to simplify a lot. For example you could adopt an idealized elastic collision with a plane model like shown in the animation below. Of course, if you make it frictionless and perfectly elastic, you won't find any limits on the velocity. If you introduce some friction, then that will determine the velocity limits. While those limits will likely differ from realistic limits, they can give you an idea would would happen in an artificial rare gas scenario.

 

[erobz]

$$ N \cos \theta = M \frac{dv_y}{dt} + \dot m ( v_y - w \cos \beta ) + \dot m w \tag{1}$$

$$ -N \sin \theta = M \frac{dv_x}{dt} + \dot m ( v_x - w \sin \beta ) \tag{2} $$

$$ \frac{v_y}{v_x} = \tan \theta \tag{3} $$

$$ \frac{dv_x}{dt}= \frac{dv_y}{dt} \frac{1}{\tan \theta} \tag{4} $$

• The frame is inertial fixed to the frictionless track.
• The wind $w$ speed is assumed constant via Bernoulli's ($P_{out} = P_{in} = P_{atm} \implies w _{out} = w_{in} = w)$
• The control volume is a black box. All we see is momentum inflows/outflows and external forces

This is standard analysis. Your claim is that there is no limit to which component of the control volumes velocity in this scenario?

 

[A.T.]

$w _{out} = w_{in}$

Do you mean the flow speed relative to control volume, or relative to a frame where the control volume moves?

 

[erobz]

Do you mean the flow speed relative to control volume, or relative to a frame where the control volume moves?

Relative to the control volume. Applying conservation of energy.

 

[A.T.]

Relative to the control volume.

If your $w$ is relative to the control volume, then the direction of $w_{in}$ is not constant, but changes as function of $v$.

What is the wind direction relative to the ground here?

 

[erobz]

If your $w$ is relative to the control volume, then the direction of $w_{in}$ is not constant, but changes as function of $v$.

What is the wind direction relative to the ground here?

It is the direction of the blue arrow at the top of the diagram pointing "down". Are you saying the momentum inflow needs to be:

$$\dot m ( v_y - w ) $$

And if I choose $w$ to be measured in the ground frame, then what? I think it is actually what I have in mind. The frames of reference are definitely a point of confusion. I would rather reference everything from ground frame to be sure. $w$ is the wind relative to the ground frame. On the way in it is fixed, and it doesn't care about the cart. On the way out, I'm not certain about conservation of energy statement now, but I want to figure that out.

 

[A.T.]

It is the direction of the blue arrow at the top of the diagram pointing "down".

If the wind relative to ground is in the negative y direction, then you are modelling upwind tacking, not downwind tacking. That's OK, as there is no theoretical limit on that either. Just making sure this is what you want.

And if I choose $w$ to be measured in the ground frame, then what?

Then $w _{out} = w_{in}$ makes no sense. Of course you have to slow down the air in the ground frame to accelerate the vehicle.

 

[erobz]

If the wind relative to ground is in the negative y direction, then you are modelling upwind tacking, not downwind tacking. That's OK, as there is no theoretical limit on that either. Just making sure this is what you want.

Thats fine by me.

Then $w _{out} = w_{in}$ makes no sense. Of course you have to slow down the air in the ground frame to accelerate the vehicle.

Then this has to be worked on. Let me think about it.

 

[erobz]

I don't see an issue with trying to work out the outgoing flow velocity using mass flowrate constraint. Mass is not accumulating in the control volume, that must be true in every frame? I would probably switch to the frame of the cart for a moment... it seems to be trickier than I originally suspected. I will probably try again tomorrow.

 

[A.T.]

I don't see an issue with trying to work out the outgoing flow velocity using mass flowrate constraint. Mass is not accumulating in the control volume, that must be true in every frame? I would probably switch to the frame of the cart for a moment... it seems to be trickier than I originally suspected. I will probably try again tomorrow.

The in/outflow rates are always based on the flow relative to the boundary, no matter what reference frame you use otherwise.

You have to distinguish ground relative and boat relative velocities clearly, and account for x & y components.

 

[erobz]

So if we switch to the frame of the cart, the flowrate entering the cart is:

$$ \dot m_{in} = \rho A ( v_y + w ) $$

And that must equal the outgoing mass flowrate in the frame of the cart ( with no mass accumulating in the control volume )

$$ \dot m_{out} = \rho A w_{out}$$

Which I believe implies:

$$w_{out} = w+v_y $$

Before switching to the inertial frame is that ok? Or does the cross-sectional area have to change? It seems a bit unsettling.

 

[A.T.]

So if we switch to the frame of the cart, the flowrate entering the cart is:

$$ \dot m_{in} = \rho A ( v_y + w ) $$

I think you have forgotten $v_x$. The inflow velocity in the cart frame is not purely vertical and the flowrate depends on the magnitude of the whole velocity vector.

 

[erobz]

I think you have forgotten $v_x$. The inflow velocity in the cart frame is not purely vertical and the flowrate depends on the magnitude of the whole velocity vector.

I think you are saying its this:

$$ w_{out} = \sqrt{( v_y + w )^2 + v_x^2 } $$

?

 

[erobz]

Updating the diagram and the system of equations to reflect the changes:$$ N \cos \theta = M \dot v_y + \dot m \left( v_y + w - \sqrt{(v_y + w )^2 + v_x^2} \cos \beta \right) \tag{1} $$

$$ -N \sin \theta = M \dot v_x + \dot m \left( v_x - \sqrt{(v_y + w )^2 + v_x^2} \sin \beta \right) \tag{2} $$

$$ v_y = v_x \tan \theta \tag{3} $$

$$ \dot v_y = \dot v_x \tan \theta \tag{4} $$

Solving the system for the limiting velocity component $v_y$ as a function of $\beta$ ( $\dot v_y = 0$ ) is get the quadratic:

$$ \left( \left( \frac{ \varphi }{ \lambda }\right)^2 - \varphi \right) v_y^2 + 2 w \left( \frac{\varphi}{ \lambda^2} - 1 \right) v_y + w^2\left( \frac{1}{\lambda^2}-1\right) = 0 $$

Here is a plot of the solution over $0^{\circ} \leq \beta \leq 44^{\circ}$ for $\theta= 45^{\circ}$:

As the outflow becomes parallel with the trajectory, the steady state velocity increases without bound. @A.T. can now rest their case, unless I've committed an error in the mechanics...I have been converted.

 

[A.T.]

As the outflow becomes parallel with the trajectory, the steady state velocity increases without bound. @A.T. can now rest their case, unless I've committed an error in the mechanics...I have been converted.

This makes sense, if I interpret your definitions correctly: $\beta$ is the flow deflection in the ground frame, right? Because in the boat frame, the flow deflection should tend towards zero in the limiting case of velocity towards infinity. This corresponds to lift/drag ratio tending towards infinity, or the aero dynamic force tending towards 90° off the relative inflow (which tends towards parallel with the trajectory too).

So now that you see that there is no theoretical limit on the upwind component, you could check the same for downwind component, for example for $\theta = 135°$. Here the relative flow has a greater range, as it changes direction by more than 90° as v goes from 0 to infinity.

 

[erobz]

This makes sense, if I interpret your definitions correctly: $\beta$ is the flow deflection in the ground frame, right?

I treated $\beta$ as the angle the flow leaves w.r.t. the control volume. i.e the flow is coming out of the boat at a constant angle $\beta$ in the frame of the boat. My momentum equations for the angle of that outflow in the ground frame would not be constant. If this is an issue, I'm not seeing it...

 

[A.T.]

I treated $\beta$ as the angle the flow leaves w.r.t. the control volume. i.e the flow is coming out of the boat at a constant angle $\beta$ in the frame of the boat. My momentum equations for the angle of that outflow in the ground frame would not be constant. If this is an issue, I'm not seeing it...

Any velocity that is parallel to the trajectory in the ground frame, is also parallel to the trajectory in the boat frame.

So for v -> infinity, the outflow velocity is parallel to the trajectory in both frames.

But the inflow is not:
- In the ground frame the inflow velocity is always vertical (true wind).
- In the boat frame (with v -> infinity) the inflow velocity is parallel to the trajectory (just like the outflow)

So the deflections (change in velocity direction) for v -> infinity are:
- In the ground frame: $\beta$
- In the boat frame: 0

 

[erobz]

Any velocity that is parallel to the trajectory in the ground frame, is also parallel to the trajectory in the boat frame.

So for v -> infinity, the outflow velocity is parallel to the trajectory in both frames.

But the inflow is not:
- In the ground frame the inflow velocity is always vertical (true wind).
- In the boat frame (with v -> infinity) the inflow velocity is parallel to the trajectory (just like the outflow)

So the deflections (change in velocity direction) for v -> infinity are:
- In the ground frame: $\beta$
- In the boat frame: 0

I don’t follow what you are trying to tell me, but I suspect it is that you believe the analysis is flawed?

 

[A.T.]

I don’t follow what you are trying to tell me, but I suspect it is that you believe the analysis is flawed?

I'm not sure, that's why I wanted to confirm if it is consistent with the result of vector analysis, which I described in post #302. Which part of it is unclear? I'm just listing the directions of the air's motion before and after the interaction for both frames of reference, in the limiting case of v -> infinity.

 

[erobz]

I'm not sure, that's why I wanted to confirm if it is consistent with the result of vector analysis, which I described in post #302. Which part of it is unclear? I'm just listing the directions of the air's motion before and after the interaction for both frames of reference, in the limiting case of v -> infinity.

It doesn’t sound like it’s consistent with what you are saying. For the analysis $\beta$ is a fixed angle. It’s dictated by the vane geometry inside the control volume that’s is turning the flow.

 

[A.T.]

For the analysis $\beta$ is a fixed angle.

Okay, but you have solved it for different values of $\beta$.

It’s dictated by the vane geometry inside the control volume that’s is turning the flow.

The vane geometry is determing how the flow relative to the vane is turned. When v -> infinite that turning angle of the relative flow should go to zero (corresponding to lift/drag -> infinity), not to 45° as indicated in your plot.

I suspect you are assuming the wrong inflow direction relative to the vane. It's not vertically down, like the true wind, but depends on v. And the vane has to be aligned with the inflow relative to the vane, so the vane orientation also depends on v. The outflow relative to the vane is then offset from the inflow relative to the vane by the vane geometry angle.

I think it would help to avoid confusion if you use different symbols for the flow in different frames, like $w$ for flow relative to the ground, and $u$ for flow relative to the vane.

 

[erobz]

Okay, but you have solved it for different values of $\beta$.

Correct. The vane is fixed relative to the cart. Just like it is in your animations... I'm saying the wind is always pointing down, what is the top speed along the track if $\beta$ is always $a,b,c \cdots$

I think it would help to avoid confusion if you use different symbols for the flow in different frames, like $w$ for flow relative to the ground, and $u$ for flow relative to the vane.

$w$ is the wind in the ground frame.

$w_{out}$ is the speed of the exiting flow in the carts frame. In the ground frame it's velocity is: $$\boldsymbol{w_{out}} =\left( v_x - \sqrt{(v_y+w)^2 + v_x^2 }\sin \beta \right) \boldsymbol{u_x} + \left( v_y - \sqrt{(v_y+w)^2 + v_x^2 } \cos \beta \right) \boldsymbol{u_y} $$

 

[A.T.]

Correct. The vane is fixed relative to the cart. Just like it is in your animations.

In my animation there is no vane, just a flat sail, which allows for elastic collision at different relative inflow directions, and thus different amounts of relative flow turning. A vane is a different model, because it fixes the relative flow turning angle.

I'm saying the wind is always pointing down, what is the top speed along the track if $\beta$ is always $a,b,c \cdots$

The true wind is always pointing down, but not the relative wind.

$w$ is the wind in the ground frame.

OK

$w_{out}$ is the exiting flow in the carts frame.

Why not call it $u_{out}$ to avoid confusion with the ground frame ?

In the ground frame it's: $$\boldsymbol{w_{out}} =\left( v_x - \sqrt{(v_y+w)^2 + v_x^2 }\sin \beta \right) \boldsymbol{u_x} + \left( v_y - \sqrt{(v_y+w)^2 + v_x^2 } \cos \beta \right) \boldsymbol{u_y} $$

This seems to still assume fixed vane? For a aligned vane $\beta$ is the angle between $\boldsymbol{u_{in}}$ and $\boldsymbol{u_{out}}$. Then $\boldsymbol{w_{out}} = \boldsymbol{u_{out}} + \boldsymbol{v}$

 

[erobz]

In my animation there is no vane, just a flat sail, which allows for elastic collision at different relative inflow directions, and thus different amounts of relative flow turning. A vane is a different model, because it fixes the relative flow turning angle.The true wind is always pointing down, but not the relative wind.OK

Why not call it $u_{out}$ to avoid confusion with the ground frame ?This seems to still assume fixed vane? For a aligned vane $\beta$ is the angle between $\boldsymbol{u_{in}}$ and $\boldsymbol{u_{out}}$. Then $\boldsymbol{w_{out}} = \boldsymbol{u_{out}} + \boldsymbol{v}$

The outflow always comes out of the control volume at a fixed angle $\beta$ relative to the control volume.

The flow field surrounding the control volume always looks something like this in the inertial frame.

You've made me "un black box" the control volume to explain the momentum exchange. It is not necessary to do so using Newton Laws.

 

[A.T.]

The flow field surrounding the control volume always looks like this in the inertial frame.

View attachment 333667

The indicated flow directions are fine for the ground frame, not for the vane frame.

The indicated vane orientation is wrong, because it must be aligned with the flow relative to the vane, not relative to the ground.

You've made me "un black box" the control volume to explain the momentum exchange. It is not necessary to do so using Newton Laws.

Then don't unmask it. But then also don't define $\beta$ in terms of vane geometry. Define it in terms of relative flow turning, as the angle between $\boldsymbol{u_{in}}$ and $\boldsymbol{u_{out}}$.

 

[erobz]

The indicated flow directions are fine for the ground frame, not for the vane frame.

The indicated vane orientation is wrong, because it must be aligned with the flow relative to the vane, not relative to the ground.Then don't unmask it. But then also don't define $\beta$ in terms of vane geometry. Define it in terms of relative flow turning, as the angle between $\boldsymbol{u_{in}}$ and $\boldsymbol{u_{out}}$.

There is something in the cv that makes the air come out of the box at a constant angle relative to the box. Are you telling me this is not allowed by the laws of physics?

 

[A.T.]

There is something in the cv that makes the air come out of the box at a constant angle relative to the box.

What do you mean by that exactly? Between which two vectors is the angle constant? Specify the frame of reference for every frame dependent vector you are using to define the angle.

 

[erobz]

What do you mean by that exactly? Between which two vectors is the angle constant? Specify the frame of reference for every frame dependent vector you are using to define the angle.

Between the wind in the ground frame and the outflow in the c.v. frame. Is there no possible entity inside the control which could make it true?

 

[A.T.]

Between the wind in the ground frame and the outflow in the c.v. frame.

And why are you defining the angle $\beta$ based on velocities from two different frames?

Is there no possible entity inside the control which could make it true?

Not a vane with fixed orientation and geometry. But if you allow those two parameters to change for different v (there is no reason why you shouldn't), then you can keep that $\beta$ you defined constant across different v. But it's not clear why you decided to keep it constant.

I also think that with this definition of $\beta$ your result from post #299 makes sense. For v -> inf the angle $\beta$ as you defined will be 45°. It's just a weird parameter, defined across different frames.

 

[Gleb1964]

With the optimal vane orientation (bisecting apparent wind angle in the moving frame), the deflected wind is moving in opposite direction to the boat speed (parallel to the boat speed, but in opposite direction). The air leaving the control volume in direction opposite to the boat speed.
Assuming that the vane angle is adjusted to the optimal at any speed, that means that at any speed the air is deflected in direction opposite to the boat moving direction. And that is valid both in the ground frame and in the boat frame.