Delta-Scuti phase folded light curve equation

[so_gr_lo]

Homework Statement:

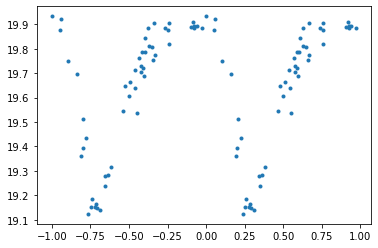
Trying to fit a model to the phase folded light curve (v-band mag vs phase) from delta-scuti v-band data, tried to find an equation relating magnitude and phase for variable stars but can't find anything, is there a specific equation I can try to fit ? I've included the equation for asymmetric sinusoidal functions but not sure thats applicable

Relevant Equations:

e.g. y=cos(x-1/2cos(x))

equation for calculating phase
[(t–to)/P]

data I'm trying to fit

 

[haruspex]

The left-right asymmetry does not seem to be the major issue. It's the up-down asymmetry that bothers me. How does it get to be so sharp at the minima?
But I'm no astrophysicist, so maybe this happens. If so, any known explanation that would suggest an equation form?

If you don't care about the physics and just want some equation that models it I'll have a go.

The thickening approaching the peak is also curious. Is it possible that your folding period isn't quite right, e.g. if you double it do you see alternating behaviours over successive peaks?

Edit: given the raw data, and the desire to express it as $y=A\sin(f(x))+B$, I would determine A and B by inspection and plot $\arcsin(\frac{y-B}A)$ against x. Of course, you will need to arrange that $|\frac{y_i-B}A|\leq 1\forall i$, either by exaggerating A or by smoothing the data.

Edit 2: I just tried that by extracting a subset of the raw data from your chart. The result looked remarkably like the raw data. Reiterating led to a series of curves tending towards a sawtooth. Of course, one does have to be careful with an ambiguity arising from arcsin, but that does not seem to be the problem.