- #1
SchroedingersLion
- 215
- 57
- TL;DR Summary
- Troubles understanding an "exotic" method of taking a derivative of a norm of a complex valued function with respect to the the real part of the function.
Greetings,
suppose we have ##h(u)=\frac{1}{2} \left\|Au-b \right\|_{2}^2## with ##A## a complex matrix and ##b,u## complex vectors of suitable dimensions. Write ##u=u_1 + iu_2## with ##u_1## and ##u_2## as the real and imaginary part of ##u##, respectively.
Show that ##\frac {\partial h} {\partial u_1} = Re \left[ A^{\dagger}(Au-b) \right]##.
Now there is a straight-forward way to show this: Just rewrite ##h(u)## in terms of the matrix/vector components, take the derivative, and show that the required result is obtained. That, however, takes 2 pages of index and dagger loaded calculations.
Our lecturer presented a simpler method, but I was unable to follow his logic (there might be errors in there):

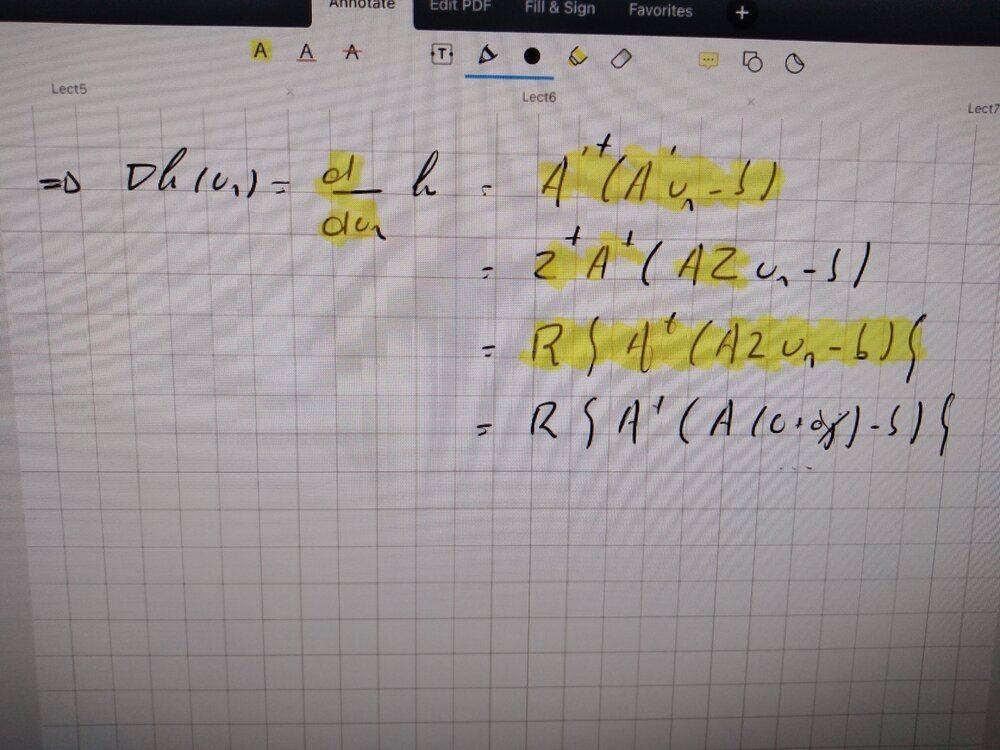
He seems to interpret ##Au## as a function, and he introduces a "zero padding" operator ##\zeta## (looks like a 2), such that ##\zeta u=u_1 + i0## (?). Though I don't see why that would lead to ##A\zeta## being a function from ##\mathbb{R}^n \rightarrow \mathbb{C}^n##. Also I feel like something is wrong with the indices of ##u## here.
Note that in the case of real-valued ##A,b,u##, the derivative becomes ##A^{\dagger}(Au-b)##, which he seems to have used at the start of image 2.
Can anyone make sense of the notes?SL
suppose we have ##h(u)=\frac{1}{2} \left\|Au-b \right\|_{2}^2## with ##A## a complex matrix and ##b,u## complex vectors of suitable dimensions. Write ##u=u_1 + iu_2## with ##u_1## and ##u_2## as the real and imaginary part of ##u##, respectively.
Show that ##\frac {\partial h} {\partial u_1} = Re \left[ A^{\dagger}(Au-b) \right]##.
Now there is a straight-forward way to show this: Just rewrite ##h(u)## in terms of the matrix/vector components, take the derivative, and show that the required result is obtained. That, however, takes 2 pages of index and dagger loaded calculations.
Our lecturer presented a simpler method, but I was unable to follow his logic (there might be errors in there):
He seems to interpret ##Au## as a function, and he introduces a "zero padding" operator ##\zeta## (looks like a 2), such that ##\zeta u=u_1 + i0## (?). Though I don't see why that would lead to ##A\zeta## being a function from ##\mathbb{R}^n \rightarrow \mathbb{C}^n##. Also I feel like something is wrong with the indices of ##u## here.
Note that in the case of real-valued ##A,b,u##, the derivative becomes ##A^{\dagger}(Au-b)##, which he seems to have used at the start of image 2.
Can anyone make sense of the notes?SL