Direction & magnitude of normal stress

[Rhaegal]

Homework Statement

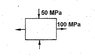
For the state of stress shown in the figure, normal stress acting on the plane of maximum shear stress is?

Homework Equations

Normal stress σ_n = σcos²θ

3. The Attempt at a Solution
Plane of maximum shear stress is 45^o relative to the max stress of 100MPa.

So the total normal stress is 75MPa (compression).

I have assume the direction of normal stresses in both the cases with respect to applied stress.
Have I assumed the direction in both cases correctly?

Thanks in advance!

 

[Orodruin]

Have I assumed the direction in both cases correctly?

No. You have not correctly taken into account that one is positive and the other negative.

I suggest looking at Mohr’s circle.

 

[Rhaegal]

No. You have not correctly taken into account that one is positive and the other negative.

I suggest looking at Mohr’s circle.

Thanks for your suggestion. I have solved it using Mohr's cirlcle and found the normal stress to be 25 MPa (Tensile).

But the problem is to be used solved using analytical approach in order to get an intuitive grasp on stress transformations. So can you please tell me how to correctly assume the direction of normal stresses with respect to my earlier approach?

 

[Orodruin]

Well, in one case it is negative and in the other positive. You get $100\cos^2(\theta) - 50 \sin^2(\theta)$ and for $\theta = \pi/4$ this translates to $(100-50)/2 = 25$ MPa.

 

[Chestermiller]

For this system, the stress tensor is given in dyadic notation by: $$\vec{\ \sigma}=\sigma_{xx}\vec{i_x}\vec{i_x}+\sigma_{yy}\vec{i_y}\vec{i_y}$$A unit normal vector to a plane of arbitrary orientation is given by: $$\vec{\ n}=\cos{\theta}\vec{i_x}+\sin{\theta}\vec{i_y}$$where $\theta$ is the angle relative to the x axis. If we dot the stress tensor with the unit normal, we obtain the traction vector on the plane: $$\vec{\ t}=\vec{\ \sigma}\centerdot \vec{\ n}=\sigma_{xx}\cos{\theta}\vec{i_x}+\sigma_{yy}\sin{\theta}\vec{i_y}$$The shear component (shear stress) of this vector on the plane is obtained by dotting the traction vector with the unit tangent to the plane: $$\vec{\ t}\centerdot \vec{i_t}=\vec{\ t}\centerdot (-\sin{\theta}\vec{i_x}+\cos{\theta}\vec{i_y})=(\sigma_{yy}-\sigma_{xx})\sin{\theta}\cos{\theta}=\frac{(\sigma_{yy}-\sigma_{xx})}{2}\sin{2\theta}$$The normal stress component of the traction vector is obtained by dotting the traction vector with the unit normal: $$\vec{\ t}\centerdot \vec{\ n}=\vec{\ t}\centerdot (\cos{\theta}\vec{i_x}+\sin{\theta}\vec{i_y})=\sigma_{xx}\cos^2{\theta}+\sigma_{yy}\sin^2{\theta}=\frac{(\sigma_{xx}+\sigma_{yy})}{2}+\frac{(\sigma_{xx}-\sigma_{yy})}{2}\cos{2\theta}$$The shear stress has maximum magnitude at $2\theta=\pi/2$. At this value of theta, the normal stress is equal to $\frac{(\sigma_{xx}+\sigma_{yy})}{2}$