- #1
Ziezi
- 3
- 0
OP warned about not using the homework template
The analytical solutions are:
\begin{equation}
\psi(x) =
\begin{cases}
Ce^{\alpha x}, \text{if } x < -\frac{L}{2}\\
Asin(kx) + Bcos(kx), \text{if } -\frac{L}{2} \leq x \leq \frac{L}{2}\\
Fe^{-\alpha x} , \text{if } x > \frac{L}{2}
\end{cases}
\end{equation}
Next, ##\psi(x)## must be continuous and differentiable, which means that the value of the functions and their derivatives must match at the boundaries, ##-\frac{L}{2}## and ##\frac{L}{2}##. Depending on whether the solution is symmetric, ##\psi(-x) = \psi(x)##, or anti-symmetric, ##\psi(-x) = -\psi(x)##, ##A = 0##, ##C = F## or ##B = 0##. ##C = -F##, respectively. For the symmetric case:
\begin{equation}
\begin{array}{|l@{}}
Fe^{-\alpha L/2} = Bcos(k L/2)\\
-\alpha F e^{-\alpha L/2} = -\alpha Bcos(k L/2)
\end{array}
\end{equation}
taking the ratio of the above two give us ##\alpha = k tan(k L/2)##. Similarly, from the anti-symmetric case we get ##\alpha = -k cot(k L/2)##.Both ##\alpha## and ##k## depend on the energy, ##E##, making the above equations transcendental. To solve them we make the following substitutions:
\begin{equation}
\begin{array}{|l@{}}
\eta = \frac{L}{2}\frac{\sqrt{2mV_0}}{\hbar}\\
\xi = \frac{L}{2}\frac{\sqrt{2mE}}{\hbar} = k \frac{L}{2} \quad (1)
\end{array}
\end{equation}
With a small rearrangement our equations for the symmetric and anti-symmetric become:
\begin{equation}
\begin{array}{|l@{}}
\alpha = k tan(k L/2) \iff \sqrt{\frac{\eta^2}{\xi^2} - 1} = tan(\xi)\\
\alpha = -k cot(k L/2) \iff \sqrt{\frac{\eta^2}{\xi^2} - 1} = -cot(\xi)
\end{array}
\end{equation}
To calculate the above I use the following Octave code:
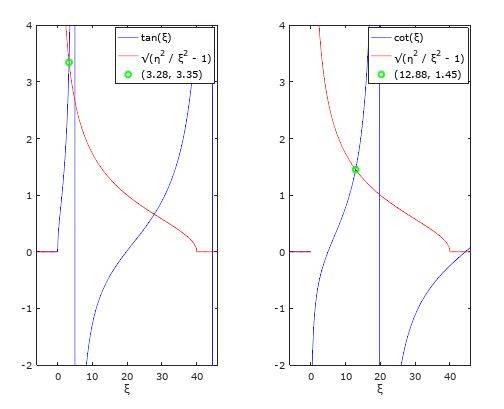
From $$(12)$$ and the two values for $$\xi$$, the results for the energies are:
> 331.98<br>
> 21.50<br>
Now, for the numerical solution I use the following:
The results for the energies are:
>36.72<br>
>27.14<br>
>12.27
I'm expecting some error but in this case, the energies differ in an order of magnitude.
Clearly, I am doing something wrong but I don't know whether the error is in the analytical or numerical solution. What am I doing wrong here? Any hint will be appreciated.
---
\begin{equation}
\psi(x) =
\begin{cases}
Ce^{\alpha x}, \text{if } x < -\frac{L}{2}\\
Asin(kx) + Bcos(kx), \text{if } -\frac{L}{2} \leq x \leq \frac{L}{2}\\
Fe^{-\alpha x} , \text{if } x > \frac{L}{2}
\end{cases}
\end{equation}
Next, ##\psi(x)## must be continuous and differentiable, which means that the value of the functions and their derivatives must match at the boundaries, ##-\frac{L}{2}## and ##\frac{L}{2}##. Depending on whether the solution is symmetric, ##\psi(-x) = \psi(x)##, or anti-symmetric, ##\psi(-x) = -\psi(x)##, ##A = 0##, ##C = F## or ##B = 0##. ##C = -F##, respectively. For the symmetric case:
\begin{equation}
\begin{array}{|l@{}}
Fe^{-\alpha L/2} = Bcos(k L/2)\\
-\alpha F e^{-\alpha L/2} = -\alpha Bcos(k L/2)
\end{array}
\end{equation}
taking the ratio of the above two give us ##\alpha = k tan(k L/2)##. Similarly, from the anti-symmetric case we get ##\alpha = -k cot(k L/2)##.Both ##\alpha## and ##k## depend on the energy, ##E##, making the above equations transcendental. To solve them we make the following substitutions:
\begin{equation}
\begin{array}{|l@{}}
\eta = \frac{L}{2}\frac{\sqrt{2mV_0}}{\hbar}\\
\xi = \frac{L}{2}\frac{\sqrt{2mE}}{\hbar} = k \frac{L}{2} \quad (1)
\end{array}
\end{equation}
With a small rearrangement our equations for the symmetric and anti-symmetric become:
\begin{equation}
\begin{array}{|l@{}}
\alpha = k tan(k L/2) \iff \sqrt{\frac{\eta^2}{\xi^2} - 1} = tan(\xi)\\
\alpha = -k cot(k L/2) \iff \sqrt{\frac{\eta^2}{\xi^2} - 1} = -cot(\xi)
\end{array}
\end{equation}
To calculate the above I use the following Octave code:
Matlab:
x = -6 : 0.1 : 46; % coordinates interval.
w = 1; % well width.
U_0 = 40; % well depth.
hbar = 1; % Planck's constant.
m = 1; % particle mass.
eta = ( w*sqrt(2*m*U_0) ) / (2*hbar); xi = @(E) ( w*sqrt(2*m * E) ) / (2*hbar);
lhs = @(E) sqrt( ( (eta*eta) ./ (xi(E).^2) ) - 1);
rhs_s = @(E) tan( xi(E) ); % symmetric case.
rhs_a = @(E) -cot( xi(E) ); % anti-symmetric case.
% Solve the transcendental equation using root-finding algorithm.
func_1 = @(E) lhs(E) - rhs_s(E); func_2 = @(E) lhs(E) - rhs_a(E);
x_0_s = 2; x_0_a = 10;
root_xi_x_s = fzero(func_1, x_0_s); root_xi_x_a = fzero(func_2, x_0_a);
root_xi_y_s = real(rhs_s(root_xi_x_s)); root_xi_y_a = real(rhs_a(root_xi_x_a));
E_0 = (2*root_xi_x_s^2) / (m * w^2); E_1 = (2*root_xi_x_a^2) / (m * w^2)
subplot(1, 2, 1);
plot(x, real(rhs_s(x)), 'b', x, real(lhs(x)), 'r', root_xi_x_s, root_xi_y_s, 'go')
axis([-6 46 -2 4])'; xlabel('\xi');
label3 = ['(', sprintf("%.2f", root_xi_x_s), ', ', sprintf("%.2f", root_xi_y_s), ')'];
legend('tan(\xi)', '\surd(\eta^2 / \xi^2 - 1)', label3);
subplot(1, 2, 2);
plot(x, real(rhs_a(x)), 'b', x, real(lhs(x)), 'r', root_xi_x_a, root_xi_y_a, 'go')
axis([-6 46 -2 4]); xlabel('\xi');
label4 = ['(', sprintf("%.2f", root_xi_x_a), ', ', sprintf("%.2f", root_xi_y_a), ')'];
legend('cot(\xi)', '\surd(\eta^2 / \xi^2 - 1)', label4);From $$(12)$$ and the two values for $$\xi$$, the results for the energies are:
> 331.98<br>
> 21.50<br>
Now, for the numerical solution I use the following:
Matlab:
% Parameters for solving problem in the interval -L < x < L.
L = 5; % Interval Length.
N = 1000; % No of points.
x = linspace(-L, L, N)'; % Coordinate vector
dx = x(2) - x(1); % Coordinate step
% Finite square well of width 2w and depth given by U_0.
U_0 = 40; w = L / 10;
U = -U_0*(heaviside(x + w) - heaviside(x - w));
% Discretized (three-point finite-difference) representation of the Laplacian.
e = ones(N, 1);
Lap = spdiags([e -2*e e], [-1 0 1], N, N)
% Total Hamiltonian
hbar = 1;
m = 1;
H = -1/2*(hbar^2 / m)*Lap + spdiags(U, 0, N, N); % T = H + U.
% Find (first 3) (smalest algebraic) eigenvalues.
nmodes = 3; options.disp = 0;
[V, E] = eigs(H, nmodes, 'sa' , options);
[E, ind] = sort(diag(E));
EThe results for the energies are:
>36.72<br>
>27.14<br>
>12.27
I'm expecting some error but in this case, the energies differ in an order of magnitude.
Clearly, I am doing something wrong but I don't know whether the error is in the analytical or numerical solution. What am I doing wrong here? Any hint will be appreciated.
---
