Does a metric exist for this surface?

[DAirey]

I have a surface defined by the quadratic relation:$$0=\phi^2t^4-x^2-y^2-z^2$$Where $\phi$ is a constant with units of $km$ $s^{-2}$, $t$ is units of $s$ (time) and x, y and z are units of $km$ (space). The surface looks like this:

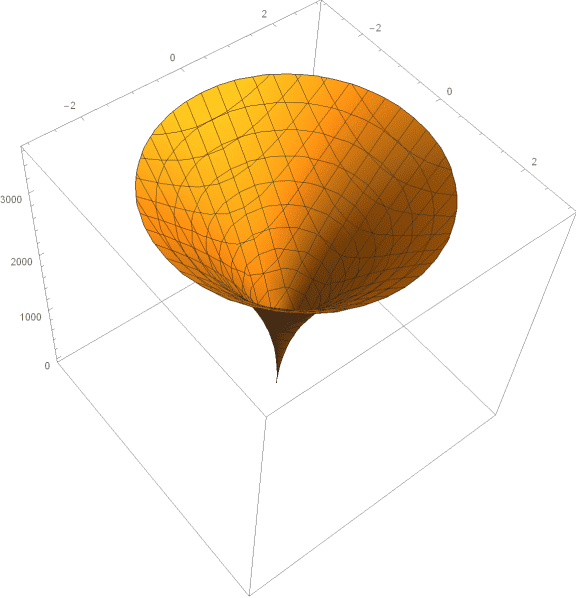
Since the formula depends on the absolute value of $t$, is it possible to create a metric to describe this surface? If so, what would the metric be (it seems to me that the metric would have to be a function of time such that $ds^2(t)=<some expression>$).

 

[Orodruin]

It is a submanifold of $\mathbb{R}^4$ so clearly you can find a metric by using the induced metric from the embedding.

 

[DAirey]

It is a submanifold of $\mathbb{R}^4$ so clearly you can find a metric by using the induced metric from the embedding.

Clearly you don't know the limits of my Differential Geometry skills. Could you walk me though the basics? I'm about halfway through the discussion of curvature in the Gravity book, so explain it like I'm an idiot. Is this a difficult problem or easy one for someone skilled in Differential Geometry? Is the metric some function of t (e.g. $ds^2(t) = <some expression>$). Most importantly, I can draw the shape using a graphics package, so intuitively I think there is a curvature. My main goal here is to express the curvature of this space (possibly as a function of time, if that's appropriate).

 

[Orodruin]

Are you looking for a Riemannian (positive definite) or a Lorentzian (signature +--- or -+++, depending on convention) metric? While you can always find a Riemannian metric based on the embedding of a manifold into a higher-dimensional Euclidean space, it is not always possible to find a Lorentzian metric based on an embedding in a higher dimensional Minkowski space.

There is a lot that can be said about the formalism for finding the induced metric. Technically it is the pullback of the metric in the higher-dimensional space, but more hands-on you essentially differentiate the expressions for the higher-dimensional coordinates in terms of the coordinates on the manifold and insert it into the higher-dimensional metric.

For example, you could find the standard metric on the unit sphere based on its embedding into $\mathbb R^3$ as follows:
The embedding using standard coordinates is given by
$$
x = \sin(\theta) \cos(\varphi), \quad y = \sin(\theta)\sin(\varphi), \quad z = \cos(\theta)
$$
leading to
$$
dx = \cos(\theta)\cos(\varphi) d\theta - \sin(\theta)\sin(\varphi) d\varphi, \quad
dy = \cos(\theta)\sin(\varphi) d\theta + \sin(\theta)\cos(\varphi)d\varphi, \quad
dz = -\sin(\theta) d\theta.
$$
Squaring and summing gives you the induced line element
$$
ds^2 = dx^2 + dy^2 + dz^2 = d\theta^2 + \sin^2(\theta) d\varphi^2 \equiv g_{ab} dy^a dy^b,
$$
which should be the familiar line element on the unit sphere and you can directly read off the elements of the induced metric tensor.

The reason this can fail to give you a Lorentzian metric when embedded in a higher-dimensional Minkowski space (or a space with signature ++---... or similar) is that you are not guaranteed that an arbitrary embedding will give you a fixed signature, or even that it will be non-degenerate. You would have to check this.

 

[DAirey]

Are you looking for a Riemannian (positive definite) or a Lorentzian (signature +--- or -+++, depending on convention) metric? While you can always find a Riemannian metric based on the embedding of a manifold into a higher-dimensional Euclidean space, it is not always possible to find a Lorentzian metric based on an embedding in a higher dimensional Minkowski space.

I'm looking for a Riemannian. I'm primarily trying to find out what the curvature of this space is as a function of time. As I understand it, after defining a formula that describes the space (as in the OP), the next step is to come up with a metric for how a small unit of space changes as you navigate the surface. This is where I get stuck as x, y, z are all linear relations, but because of the quadratic nature of t, the delta of one second is not going to be the same as the delta of another second, so it looks like the metric is going to be a function of t. My best guess is something that looks like this:$$ds^2(t)=a_0^2(t^4-(dt-t)^4)-dx^2-dy^2-dz^2$$Does this appear to be right?

 

[Orodruin]

what the curvature of this space is

Which curvature? There are many possibilities that you could be referring to here. Extrinsic curvature, intrinsic curvature, the curvature tensor, ...

I believe I'm looking for a Riemannian, but to be honest, ... function of time.

The "time" suggests to me that you want something that depends on some sort of time, but it is not clear what you mean by this. Does the embedding depend on time or do you figure time is one of your coordinates? If "time" is a coordinate and you are looking for a space-time, then you want your metric to be Lorentzian. A Riemannian metric does not describe a space-time. Furthermore, $t$ is just an arbitrary coordinate. Also note that it is not clear exactly what you want to do with the relation of space and time. There is no one unique metric that will do what you want. For example, you could be looking for a FLRW-type metric where $ds^2 = dt^2 - a(t)^2 dS^2$, where $dS^2$ is the line element on the spatial part, but this is not unique if you just want a metric where $a(t) \propto t^2$.

This is where I get stuck as x, y, z are all linear relations

What do you mean by this? You have not specified any relations for x, y, and z.

a simple metric that represents the surface I've described (that is, quadratic expansion of space with time).

I think this is to a largely related to the fact that you do not seem to know exactly which question you want to ask. If you want a FLRW space-time where $a(t) \propto t^2$, you really do not want to embed it in anything and it makes little sense to write things such as $\phi^2 t^4 = x^2 + y^2 + z^2$, because that is a three-dimensional hypersurface in $\mathbb R^4$.

 

[DAirey]

Which curvature?

I apologize for not having all the base concepts needed to answer your questions specifically. Perhaps a little background would be useful. I've found that the data found in SNe Ia magnitudes matches a quadratic relation better than FLRW, so I'm working backwards from there. If the surface I describe shows how space grows quadratically as a function of time, then I would like to know what the curvature of 3-dimensional space is at time $t$.

The "time" suggests to me that you want something that depends on some sort of time, but it is not clear what you mean by this. Does the embedding depend on time or do you figure time is one of your coordinates?

Time is a coordinate.

If "time" is a coordinate and you are looking for a space-time, then you want your metric to be Lorentzian. A Riemannian metric does not describe a space-time.

OK.

Furthermore, $t$ is just an arbitrary coordinate. Also note that it is not clear exactly what you want to do with the relation of space and time. There is no one unique metric that will do what you want. For example, you could be looking for a FLRW-type metric where $ds^2 = dt^2 - a(t)^2 dS^2$

I believe that's what I'm looking for. See my edit in my previous post.

 

[Orodruin]

I've found that the data found in SNe Ia magnitudes matches a quadratic relation better than FLRW

Found where? And what assumptions? What do you mean by "a quadratic relation" here?

FLRW is a general description of an isotropic and homogeneous universe and not a single specific space-time.

I believe that's what I'm looking for. See my edit in my previous post.

The "metric" in your post unfortunately makes no sense at all. Any expanded term must have two differentials as the metric is a (0,2) tensor.

 

[FactChecker]

@Orodruin , I like your signature: "'You did not take relativity of simultaneity into account.' - The answer to 99% of all paradox threads in the relativity forum"

 

[PeterDonis]

it seems to me that the metric would have to be a function of time

The metric of a spacetime can be a function of the coordinates, and you might call one of those coordinates "time", but it's still the metric of a single 4-dimensional geometry, not a set of geometries parameterized by time.

 

[DAirey]

Found where? And what assumptions? What do you mean by "a quadratic relation" here?

The magnitude of SNe Ia act as a proxy for distance. The red-shift tells us how the universe has expanded from the time the light was emitted. These two values define an expansion history which matches a quadratic expansion better than FLRW, so I'm working backwards to see if there's a geometric explanation for the expansion history.

The "metric" in your post unfortunately makes no sense at all.

I'm not surprised it doesn't make sense. As I mentioned earlier, you're dealing with an idiot. When you calculate the distance between any two points in space, it doesn't matter where in space you are. However, the distance between any two times depends on the absolute value of $t$, so it occurs to me that the metric -- the function that describes a small distance between any two points on the surface -- is going to depend on time. The formula above is what I got when I worked out the geometry in a spreadsheet, but, again, what I'm trying to capture is the distance between two points on this surface.

Any expanded term must have two differentials as the metric is a (0,2) tensor.

It's my understanding that the term $\phi^2t^4$ has units of $km^2$, just like the rest of the terms, so why doesn't it make sense? Please show me where I went wrong.

 

[DAirey]

I think this is to a largely related to the fact that you do not seem to know exactly which question you want to ask. If you want a FLRW space-time where a(t)∝t2a(t)∝t2a(t) \propto t^2, you really do not want to embed it in anything and it makes little sense to write things such as ϕ2t4=x2+y2+z2ϕ2t4=x2+y2+z2\phi^2 t^4 = x^2 + y^2 + z^2, because that is a three-dimensional hypersurface in R4R4\mathbb R^4.

OK. I think you may be on to something here. My ultimate goal is to say, at time t, will the spatial dimensions appear to be curved when I look at far distant objects (like CMB). Don't I need a metric for that?

 

[Orodruin]

The magnitude of SNe Ia act as a proxy for distance. The red-shift tells us how the universe has expanded from the time the light was emitted. These two values define an expansion history which matches a quadratic expansion better than FLRW, so I'm working backwards to see if there's a geometric explanation for the expansion history.

I think there is clearly something you are not understanding here. The magnitude of type Ia supernovae act as a proxy for the luminosity distance. The relation between red-shift, luminosity distance, and the expansion history of the universe is a non-trivial one. It is unclear to me how you have fitted this data.

When you calculate the distance between any two points in space, it doesn't matter where in space you are

It is unclear to me what you want to say with this.

However, the distance between any two times depends on the absolute value of t, so it occurs to me that the metric -- the function that describes a small distance between any two points on the surface -- is going to depend on time.

I am sorry, but you clearly do not have the prerequisites to do this calculation, nor the calculation of the relationship between redshift, luminosity distance, and expansion history. As @PeterDonis pointed out, you cannot separate time from space-time. The FLRW universe is an integral part of the computation.

so why doesn't it make sense? Please show me where I went wrong.

This would require a minor university course in differential geometry. At an online discussion forum, I can give no other advice than to take one or to acquire the corresponding knowledge by other means. It is not clear to me what your current knowledge of university level mathematics are, so I cannot tell you exactly where to start.

OK. I think you may be on to something here. My ultimate goal is to say, at time t, will the spatial dimensions appear to be curved when I look at far distant objects (like CMB). Don't I need a metric for that?

Unfortunately, this makes no sense. As already pointed out in this thread, $t$ is just a coordinate in space-time. You cannot separate time from space-time the way you seem to want to.

 

[PeterDonis]

It's my understanding that the term $\phi^2t^4$ has units of $km^2$, just like the rest of the terms

We're not talking about the equation you wrote in your OP. That's not a metric. It's just an equation that the coordinates of the surface have to satisfy. It doesn't tell you the distance between neighboring points on the surface.

You still don't appear to be clear about what you are looking for. There are basically two possibilities:

(1) You are looking for a Lorentzian metric for a 4-dimensional spacetime. An example of such a metric is:

$$
ds^2 = - dt^2 + a^2(t) \left( dx^2 + dy^2 + dz^2 \right)
$$

This is the metric of an FRW universe with flat spacelike surfaces of constant time; that is, each surface of constant $t$ is a flat Euclidean 3-dimensional space. The only difference between any two such spaces is the scale factor $a(t)$, which is a function of $t$. But note that the metric as a whole is not a function of $t$; only the scale factor is.

(2) You are looking for a Riemannian metric for a 3-dimensional space; more precisely, for a parameterized family of metrics for a parameterized family of 3-dimensional spaces, where the parameter is a thing called $t$, which you are interpreting as "time". An example of such a family of metrics would be:

$$
ds^2 = a^2(t) \left( dx^2 + dy^2 + dz^2 \right)
$$

Note that this looks just like the spatial part of the FRW metric I wrote down above; but here, we are not interpreting this as a single metric of a single geometric spacetime, we are interpreting it as a family of metrics for a family of geometric spaces. (And, of course, all of these spaces are flat Euclidean spaces, so this metric doesn't describe the surface you are interested in.)

Also note that in these metrics, each term some coefficient times the differential of one of the coordinates (i.e., $dt$, $dx$, $dy$, or $dz$). There are no terms that are not of that form. The "metric" you wrote down in post #5 does not have that form; there are terms in it that involve $t$ but don't have any coordinate differential in them. (And of course the expression you wrote down in your OP has no coordinate differentials at all, anywhere.) That's why it doesn't make sense as a metric.

Also note that you appear to be interested in a single surface, not a family of surfaces, because you only drew one surface in your OP. But that surface is a 3-dimensional surface, not a 4-dimensional one: the equation you wrote in your OP describes a 3-dimensional surface embedded in a 4-dimensional space. But you talk about finding a metric that is a function of time, which implies that you are looking for a family of metrics parameterized by time, not the metric of a single surface. So it appears to me that you are somewhat confused about what you are actually looking for.

 

[PeterDonis]

The magnitude of SNe Ia act as a proxy for distance. The red-shift tells us how the universe has expanded from the time the light was emitted. These two values define an expansion history which matches a quadratic expansion better than FLRW, so I'm working backwards to see if there's a geometric explanation for the expansion history.

First, please review the PF rules on personal theories, because it looks like that's what you are pursuing here.

Second, it is not at all clear how whatever you think you are doing with the surface you described in your OP is even relevant to the stated goal in the above quote.

Is this a difficult problem or easy one for someone skilled in Differential Geometry?

It's not clear what actual problem you think you are trying to solve. The problem of determining the spacetime geometry of the universe is not easy, but people skilled in Differential Geometry have made good progress on it. But it's not clear that that's the problem you think you are working on.

Moreover, the question here is not whether this general subject is difficult or easy for someone skilled in Differential Geometry; the question is whether it is difficult or easy for you. Unfortunately, as @Orodruin has said, it appears that it is way too difficult for you at your current level of understanding. So the best advice we can give you is to not even try to figure stuff like this out until you have attained a much better understanding, by just trying to learn what our current cosmology says instead of trying to second guess it.

And with that, this thread is closed.