- #1
LCSphysicist
- 645
- 161
- Homework Statement
- All below
- Relevant Equations
- All below
Say... A ball is moving to the right, and we want to say that it doesn't slip.
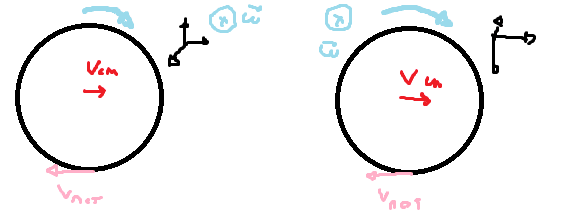
My doubt is, in which case we put
Vrot = - Vcm = - α*r
or
Vrot = Vcm = α * r
My doubt is, in which case we put
Vrot = - Vcm = - α*r
or
Vrot = Vcm = α * r
Last edited: