Elastic potential energy of a hanging cone

[Saitama]

Homework Statement

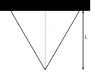
A cone of circular cross section having base radius R, mass M and height L is suspended from its base as shown in figure. The material of cone has Young's modulus Y. If the elastic potential energy stored in the cone can be expressed as:
$$E=\frac{m^ag^bL^c}{d\pi^eY^fR^g}$$
Then find a+b+c+d+e+f+g.

Homework Equations

The Attempt at a Solution

Since the question doesn't specify whether the cone is hollow or solid, I assumed it as solid and proceeding with this assumption gave me a close answer.

From a distance $x$ above the apex of the cone, I selected a disk (or frustum) of thickness $dx$. The force responsible for the elongation of this small part is:
$$F=\rho\frac{1}{3}\pi r^2 xg$$
where $r$ is the radius of selected disk. Hence, elongation $dl$ is:
$$dl=\frac{Fdx}{AY}=\frac{\rho \pi r^2xg \,dx}{3Y \pi r^2}=\frac{\rho g}{3Y}x\,dx$$
The elastic potential energy stored in this part is:
$$dE=\frac{1}{2}\frac{YA}{dx}\,dl^2=\frac{1}{2}\frac{Y\pi r^2}{dx}\,dl^2$$
I plugged in $r=x(R/L)$ and the expression for $dl$ and integrated within $x$ from 0 to L. I got the following expression:
$$E=\frac{m^2g^2L}{10Y\pi R^2}$$
The above expression gives me 19 as the answer but the correct answer is 18.

I think there is something wrong with my initial assumptions and working.

Any help is appreciated. Thanks!

 

[paisiello2]

Yes, I get the same 19.

 

[haruspex]

The above expression gives me 19 as the answer but the correct answer is 18.

Your working all looks correct to me. I get the same answer.

 

[Saitama]

Your working all looks correct to me. I get the same answer.

Yes, I get the same 19.

Thanks both of you!

Is it possible to solve the problem for a hollow cone? If so, can I please have a few hints?

 

[haruspex]

Thanks both of you!

Is it possible to solve the problem for a hollow cone? If so, can I please have a few hints?

Yes, of course. You need to assume some small constant thickness, giving you a different expression for suspended mass and cross-sectional area.
But note that your equation is dimensionally correct. This means it is not possible to arrive at 18 by changing a single exponent unless it is the exponent on pi. Changing the 10 to a 9 is just possible, I suppose.

 

[Saitama]

Yes, of course. You need to assume some small constant thickness, giving you a different expression for suspended mass and cross-sectional area.

I am having trouble visualiaing the case of hollow cone. I select a frustum at distance $x$ along the slant height from tip. The height of frustum is $dx\,\cos\theta$ where $\theta=\arctan(R/L)$. The force "stretching" this part is along the slant height. I call it T. Hence,
$$dl=\frac{T\,dx}{YA}$$
I am confused about what should I fill in for A. :(

 

[haruspex]

I am having trouble visualiaing the case of hollow cone. I select a frustum at distance $x$ along the slant height from tip. The height of frustum is $dx\,\cos\theta$ where $\theta=\arctan(R/L)$. The force "stretching" this part is along the slant height. I call it T. Hence,
$$dl=\frac{T\,dx}{YA}$$
I am confused about what should I fill in for A. :(

The thickness d will be at angle theta to the horizontal. The distance around the frustum is 2πx sin(θ). A is the product of the two.

 

[Saitama]

The thickness d will be at angle theta to the horizontal. The distance around the frustum is 2πx sin(θ). A is the product of the two.

What is d? What thickness are you talking about?

 

[haruspex]

What is d? What thickness are you talking about?

As I said in an earlier post, you need to assume some small thickness for the wall of the hollow cone. It should cancel out later.

 

[Saitama]

As I said in an earlier post, you need to assume some small thickness for the wall of the hollow cone. It should cancel out later.

Why $d$ is at an angle?

Do you mean $A=2\pi x\sin\theta d$. What to fill in for T? The T acts along the slant height, would it be correct to write:
$$T\cos\theta=\rho \pi (x\sin\theta)xdg$$

 

[haruspex]

Why $d$ is at an angle?

Because the wall of the cone is at an angle. The thickness, by definition, is he shortest distance across the wall.

Do you mean $A=2\pi x\sin\theta d$.

Yes

What to fill in for T? The T acts along the slant height, would it be correct to write:
$$T\cos\theta=\rho \pi (x\sin\theta)xdg$$

Looks right.

 

[Saitama]

Because the wall of the cone is at an angle. The thickness, by definition, is he shortest distance across the wall.
Yes

Looks right.

I proceeded further but $d$ doesn't seem to cancel out.
$$dE=\frac{1}{2}\frac{YA}{dx}dl^2=\frac{dx}{YA}T^2$$
From my previous post,
$$T=\rho \pi x^2\tan\theta dg$$
Plugging this in dE gives me a d^2 in the numerator and d in the denominator. This means that $d$ doesn't cancel out. Did I go wrong somewhere?

 

[haruspex]

I proceeded further but $d$ doesn't seem to cancel out.
$$dE=\frac{1}{2}\frac{YA}{dx}dl^2=\frac{dx}{YA}T^2$$
From my previous post,
$$T=\rho \pi x^2\tan\theta dg$$
Plugging this in dE gives me a d^2 in the numerator and d in the denominator. This means that $d$ doesn't cancel out. Did I go wrong somewhere?

No, I think it means the cone is not hollow.

 

[Saitama]

No, I think it means the cone is not hollow.

Sorry, I didn't understand.

I already solved the case of solid cone and you agreed with my answer. We are solving for the hollow case. :)

 

[haruspex]

Sorry, I didn't understand.

I already solved the case of solid cone and you agreed with my answer. We are solving for the hollow case. :)

The OP did not specify whether the cone is hollow or solid. Presumably it intended one or the other, and it was always a fair bet that it should be solid. When that did not produce the book answer, you embarked on solving the hollow case - fair enough, but always a bit of a long shot. But that has not produced even the right form of answer, let alone the right numbers, so we can rule that out.
The conclusion is that either the book answer is wrong, or we've both made a mistake in analysis of the solid case.

 

[AlephZero]

The answer for a hollow cone must depend on the thickness of the cone (as your formulas showed).

Suppose you keep everything constant except for the thickmess. (The density of the material has to change, to keep the mass constant)

If you double the thickness, the stress at any point will be halved, so the strain energy density will reduce by 1/4. But there is twice as much volume, so the strain energy will be halved. So the strain energy is inversely proportional to the thickness.

For the solid cone, you can simplify the OP's solution a bit if you see that:

The total mass is M, so the mass up to height $x$ must be $Mx^3/L^3$.

The area of the "base" is $\pi R^2$, so the area at height $x$ is $\pi R^2 x^2 / L^2$.

Then find the stress, strain, and strain energy density as functions of $x$, and integrate the strain energy density over the volume.

That gave me the same same answer as the OP, 19.

 

[Saitama]

Thanks both of you!

I would prefer to agree with your answer instead of the book. :)