Equations of relative motion with respect to a rotating reference frame

[Master1022]

Homework Statement

How to use these equations of motion

Relevant Equations

$r = R + \rho$
$\dot r = \dot R + (\Omega \times \rho) + \dot \rho$
$\ddot r = \ddot R + \ddot \rho + 2(\Omega \times \dot \rho) + \dot \Omega \times \rho + \Omega \times (\Omega \times \rho)$

Hi,

I am just writing a post to follow up on a previous thread I made which I don't think was very clear. The question is mainly about how to use the below equations when there is also a rotation of the body around the fixed reference point.

Please see the diagram here to see how the vectors have been defined:

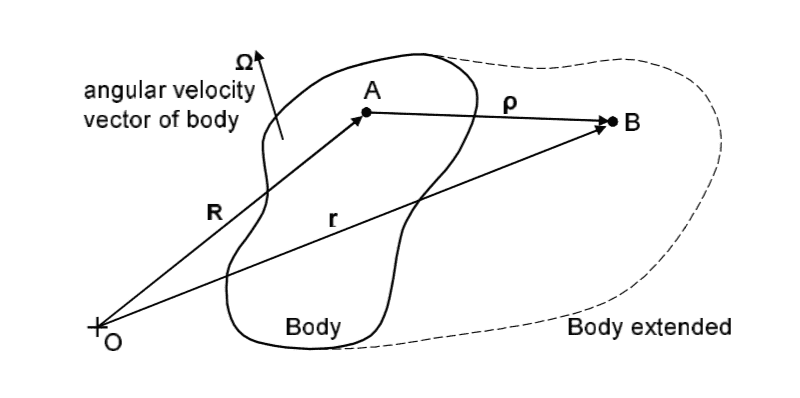
We can then derive the following equations of motion:
$$ r = R + \rho $$
$$ \dot r = \dot R + (\Omega \times \rho) + \dot \rho $$
$$ \ddot r = \ddot R + \ddot \rho + 2(\Omega \times \dot \rho) + \dot \Omega \times \rho + \Omega \times (\Omega \times \rho) $$

However, what happens if there is also a rotation of A around O (lets say that the angular velocity is $\omega$)? How do we now use the equations to find the absolute velocity and acceleration of B?

My approach:
In an attempt to be clear and not keep re-using terms, let us define $\alpha$ to be the rotation of the body (about A) relative to the the rotation of A around O and $\omega$ is defined above.

Velocity:
The equation is:
$$ \dot r = \dot R + (\Omega \times \rho) + \dot \rho $$
Does $\dot R$ include the rotation of point A around O and therefore become $\dot R = (\omega \times R)$? I originally thought that vector only included a linear translational velocity...

Now for the other two terms, one problem I was working seems to suggest that the rotation of B around point A is included in the $\dot \rho$ term and not the $(\Omega \times \rho)$ term. Therefore, it suggests that $\dot \rho = (\alpha \times \rho)$ where $\alpha$ is defined as above. It also suggests that $(\Omega \times \rho) = (\omega \times \rho)$. I am struggling to understand why this is the case.

Acceleration:
The equation is:
$$ \ddot r = \ddot R + \ddot \rho + 2(\Omega \times \dot \rho) + \dot \Omega \times \rho + \Omega \times (\Omega \times \rho) $$

the $\ddot R$ term contains $\omega \times (\omega \times R) + \dot \omega \times R$ (it would also contain any linear relative acceleration but there is none).

the $2(\Omega \times \dot \rho)$ is the Coriolis term which is $2(\omega \times \dot \rho)$ where $\dot \rho$ has been calculated above. This term makes sense to me.

the $\ddot \rho$ term contains the $\alpha \times (\alpha \times \rho) + \dot \alpha \times \rho$

the $\dot \Omega \times \rho$ term is $\dot \omega \times \rho$

the $\Omega \times (\Omega \times \rho) = \omega \times (\omega \times \rho)$

I am also struggling to see why the last two terms relate $\omega$ and $\rho$.

Any correction/ clarification is greatly appreciated. In the lecture notes, we only saw situations with $R = 0$ and body just rotating around a fixed point, so this is new to me.

Thanks

 

[FactChecker]

I recommend that you only worry about one rotation and coordinate change at a time. If you understand each one, keep it simple. There are situations that require one coordinate transformation after another, after another,... IMO, the combination of them all would be very complicated and virtually incomprehensible.

 

[Master1022]

I recommend that you only worry about one rotation and coordinate change at a time. If you understand each one, keep it simple. There are situations that require one coordinate transformation after another, after another,... IMO, the combination of them all would be very complicated and virtually incomprehensible.

Thanks for your response @FactChecker . However, I found a diagram for these types of problems:

and this question asks us to find the absolute velocity and acceleration of A. We are given the distances, $\theta$, $\dot \theta$, $\ddot \theta$, $\alpha$, $\dot \alpha$, and $\ddot \alpha$. In this situation we need to consider both rotations together and the solution uses the same method as above.

For example, the acceleration is equation is turned from

$$ \ddot r = \ddot R + \ddot \rho + 2(\Omega \times \dot \rho) + \dot \Omega \times \rho + \Omega \times (\Omega \times \rho) $$
into
$$ a_A = a_o + 2 \dot \theta \times v_{A/o} + \ddot \theta \times r_{A/o} + a_{A/o} + \dot \theta \times \dot \theta \times r_{A/o} $$
and am confused why $\dot \theta \times \dot \theta \times r_{A/o}$ appears in the equation. The terms like $\dot \alpha \times \dot \alpha \times r_{A/o}$ are contained within $a_{A/o}$

 

[TSny]

For example, the acceleration is equation is turned from

$$ \ddot r = \ddot R + \ddot \rho + 2(\Omega \times \dot \rho) + \dot \Omega \times \rho + \Omega \times (\Omega \times \rho) $$
into
$$ a_A = a_o + 2 \dot \theta \times v_{A/o} + \ddot \theta \times r_{A/o} + a_{A/o} + \dot \theta \times \dot \theta \times r_{A/o} $$
and am confused why $\dot \theta \times \dot \theta \times r_{A/o}$ appears in the equation.

If you rearrange the term $a_{A_0}$ in the second equation, then the two equations are$$\ddot r = \ddot R + \ddot \rho + 2(\Omega \times \dot \rho) + \dot \Omega \times \rho + \Omega \times (\Omega \times \rho) $$

$$ a_A = a_o + a_{A/o} + 2 \dot \theta \times v_{A/o} + \ddot \theta \times r_{A/o} + \dot \theta \times \dot \theta \times r_{A/o} $$

Each term in the second equation equals the corresponding term in the first equation.

Note that $\Omega$ in this picture

corresponds to $\dot \theta$ in this picture

The square plate corresponds to the "body" in the first picture. The angular velocity of the square plate relative to the inertial frame XOY is $\dot \theta$, and this corresponds to $\Omega$ in the first picture. The particle A in the second picture corresponds to the particle B in the first picture. The point o in the second picture corresponds to point A (fixed in the body) in the first picture. Point O in the second picture corresponds to point O in the first picture.

 

[Master1022]

If you rearrange the term $a_{A_0}$ in the second equation, then the two equations are$$\ddot r = \ddot R + \ddot \rho + 2(\Omega \times \dot \rho) + \dot \Omega \times \rho + \Omega \times (\Omega \times \rho) $$

$$ a_A = a_o + a_{A/o} + 2 \dot \theta \times v_{A/o} + \ddot \theta \times r_{A/o} + \dot \theta \times \dot \theta \times r_{A/o} $$

Each term in the second equation equals the corresponding term in the first equation.

Note that $\Omega$ in this picture
View attachment 269948

corresponds to $\dot \theta$ in this picture
View attachment 269949
The square plate corresponds to the "body" in the first picture. The angular velocity of the square plate relative to the inertial frame XOY is $\dot \theta$, and this corresponds to $\Omega$ in the first picture. The particle A in the second picture corresponds to the particle B in the first picture. The point o in the second picture corresponds to point A (fixed in the body) in the first picture. Point O in the second picture corresponds to point O in the first picture.

Thank you @TSny very much for the explanation! Can you explain what the physical interpretation of the $\dot \theta \times \dot \theta \times r_{A/o}$ term is? It looks like a centripetal-type of acceleration term, but I am not really sure how to explain it in words.

 

[TSny]

Can you explain what the physical interpretation of the $\dot \theta \times \dot \theta \times r_{A/o}$ term is? It looks like a centripetal-type of acceleration term, but I am not really sure how to explain it in words.

Yes, this term is a centripetal-type acceleration. Suppose the particle A is not moving relative to the plate, so A is at a fixed location on the circular track and $\alpha$ is not changing. The particle will still experience acceleration due to the rotation of the plate about the corner O. The centripetal part of this acceleration is $\dot \theta \times ( \dot \theta \times r_{A/O} )$. Write $r_{A/O}$ as $r_{A/O} = r_{o/O}+r_{A/o}$. The acceleration is then

$\dot \theta \times \left( \dot \theta \times ( r_{o/O}+r_{A/o}) \right) = \dot \theta \times ( \dot \theta \times r_{o/O} ) + \dot \theta \times ( \dot \theta \times r_{A/0} )$

The last term on the right is the term you are asking about. The first term on the right is contained in $a_o$ in the overall expression

$$ a_A = a_o + a_{A/o} + 2 \dot \theta \times v_{A/o} + \ddot \theta \times r_{A/o} + \dot \theta \times (\dot \theta \times r_{A/o} )$$

 

[Master1022]

Yes, this term is a centripetal-type acceleration. Suppose the particle A is not moving relative to the plate, so A is at a fixed location on the circular track and $\alpha$ is not changing. The particle will still experience acceleration due to the rotation of the plate about the corner O. The centripetal part of this acceleration is $\dot \theta \times ( \dot \theta \times r_{A/O} )$. Write $r_{A/O}$ as $r_{A/O} = r_{o/O}+r_{A/o}$. The acceleration is then

$\dot \theta \times \left( \dot \theta \times ( r_{o/O}+r_{A/o}) \right) = \dot \theta \times ( \dot \theta \times r_{o/O} ) + \dot \theta \times ( \dot \theta \times r_{A/0} )$

The last term on the right is the term you are asking about. The first term on the right is contained in $a_o$ in the overall expression

$$ a_A = a_o + a_{A/o} + 2 \dot \theta \times v_{A/o} + \ddot \theta \times r_{A/o} + \dot \theta \times (\dot \theta \times r_{A/o} )$$

@TSny - thank you once again, that makes much more sense now! I haven't been able to find such a clear explanation anywhere else.

Thanks

 

[TSny]

Ok. Glad I could help.