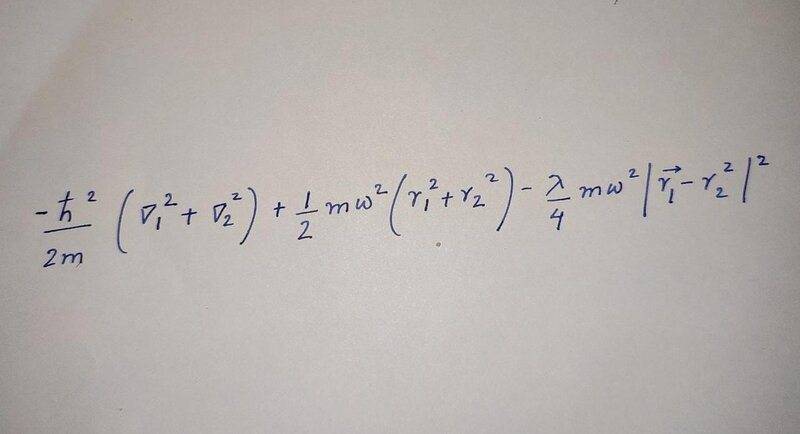Find Ground State Energy of 3D Harmonic Oscillator

[koustav]

Summary:: I am trying to find the exact ground state energy of the hamiltonian.kindly help me with this

 

[stevendaryl]

I suggest rewriting your equation in terms of new variables:

$\vec{R} = \frac{1}{2} (\vec{r}_1 + \vec{r}_2)$
$\vec{r} = \vec{r}_1 - \vec{r}_2$

 

[Haborix]

To the OP, would you clarify the typo in the last term, just so we are all certain what we're working with.

 

[koustav]

To the OP, would you clarify the typo in the last term, just so we are all certain what we're working with.

there will be vector sign and no square on the last term

 

[Haborix]

Thank you. Stevendaryl's suggestion is a good one, give it a try and let us know how you get along. The goal of that kind of substitution is to get a Hamiltonian which separates into a sum two Hamiltonians, one in the $R$ coordinate and the other in the $r$ coordinate.