Find the equivalent resistance of this circuit

[zenterix]

Homework Statement

Find the equivalent resistance of this circuit (Problem 2.3 of Chapter 2 of Agarwal's Foundations of Analog and Digital Electronic Circuits.

Relevant Equations

I will use symmetry.

Consider the following circuit where all resistors have resistance $1 \Omega$.

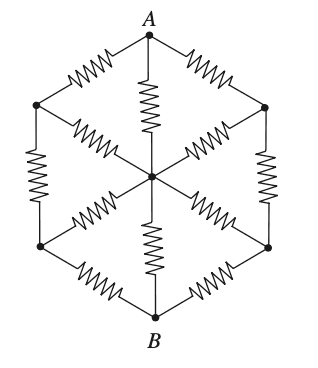
We would like to find the equivalent resistance.

My solution differs from the answer at the end of the book I am reading, so I would like to know what I did wrong, or if the book is wrong.

Here is what I did

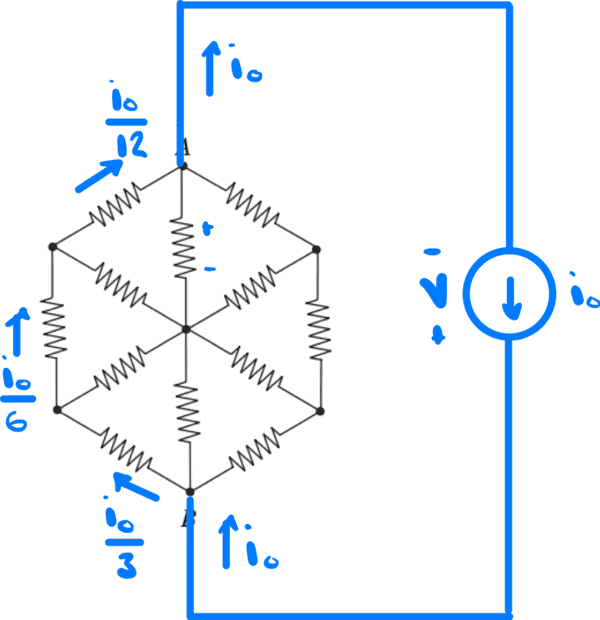
I used symmetry to determine the currents on the resistors.

Then I used KVL on the loop that includes these outer resistors and passing through the current source, assuming that the potential difference between a point below the current source (+) and a point above it (-) is V.

$\frac{i_0}{3}+\frac{i_0}{6}+\frac{i_0}{12}-V=0$

$V=\frac{7i_0}{12}=i_0R_{eq}$

$R_{eq}=\frac{7}{12}\Omega$

This seems right to me, but the book says the answer is $\frac{4}{5}\Omega$

What am I missing?

 

[DaveE]

Please explain how you determined the current $i_o/3$.

 

[zenterix]

Please explain how you determined the current $i_o/3$.

This question immediately showed me where I was going wrong. There is symmetry in the problem but not the symmetry I was using.

The symmetry of the currents is as follows

The right and left sides are symmetrical (same currents, resistances, and voltages), but we need independent current (and voltage) variables for the two resistors in the middle.

The next step is to write out seven independent equations in the seven unknown currents.

We have seven total nodes, but the two on the left are exactly the same as the two on the right in terms of equations. Thus, we have five nodes with different equations, but only four are independent equations.

For the three remaining equations, we can use the three small loops on the left side.

The algebra is long and error-prone (I went through it and made mistakes). I decided to put the system in a matrix and use Maple to solve.

Here are the calculations

and this system of equations in matrix form (augmented matrix [A b] from Ax=b)

the solution to which is

Now that we have all the currents (the vector above represents $i_1,i_1,...,i_7$), we can use KVL on a loop that includes the current source.

For example,

$i_1+i_4+i_5=\frac{4}{5}i_0=V=i_0R_{eq}$

$R_{eq}=\frac{4}{5}\Omega$

 

[DaveE]

OK. I didn't solve it and I'm a bit too lazy to check the details of your work.

However, There are more symmetries than just the A-B axis. You should be able to reduce the dimensionality of your equations. For example, what if $i_1 \neq i_5$?

Also, there's nothing wrong with looking for symmetric currents. Most people would look at the voltages first. It's essentially the same problem. I would prefer voltages, but that wouldn't make it easier.

 

[alan123hk]

According to the principle of symmetry, the calculation result I got is 0.8 Ohm, so I think the answer listed in that book is correct.

 

[alan123hk]

Now that we have all the currents (the vector above represents i1,i1,...,i7), we can use KVL on a loop that includes the current source.

The algebra is long and error-prone (I went through it and made mistakes). I decided to put the system in a matrix and use Maple to solve.

I think the method you used is more rigorous, but also more complicated.
In fact, you can calculate the answer in a very simple way, just by dividing the entire circuit into two parts, either vertically or horizontally.

For example, split it into two parts horizontally

 

[DaveE]

I think the method you used is more rigorous, but also more complicated.
In fact, you can calculate the answer in a very simple way, just by dividing the entire circuit into two parts, either vertically or horizontally.

For example, split it into two parts horizontallyView attachment 333126

You can also reduce it again with symmetry about the vertical axis which will give you R'=2||(1+1||(1/2))=0.8.
Then the whole network is four R' in a series parallel arrangement so R=R'=0.8.
But I don't think this last step makes the calculation much easier.

 

[alan123hk]

Yes, we can cut the circuit into two parts that are vertically symmetrical or horizontally symmetrical.
Interestingly, cutting a vertically connected resistor horizontally will give you half the resistance value, and cutting a vertically connected resistor vertically will give you double the resistance value.

 

[DaveE]

This problem is typical of physics or beginning EE problem sets, but will rarely be see in practice by reals EEs. However, I think it illustrates a very important and useful concept that is used in practice frequently. It is this: do as much as you can to reduce the complexity of the network in question before you start writing KCL & KVL equations. Usually this is done with Norton and Thevenin source transformations. Many linear networks can be mostly solve by repeated sketches of simplifying substitutions with very little math.

 

[zenterix]

I think the method you used is more rigorous, but also more complicated.
In fact, you can calculate the answer in a very simple way, just by dividing the entire circuit into two parts, either vertically or horizontally.

For example, split it into two parts horizontallyView attachment 333126

Interesting approach.

Seems you are splitting as follows

and calculating the resistance of the blue part as one thing and then multiplying it by two. I think this multiplication by two is because you are considering the blue in series with the red. Is this so?

I don't see, technically speaking, why you can consider, for example, the left side of the blue part to be 1 + (1 || 1/2) since the wires after the (1 || 1/2) aren't connected together.

This is the same reason why I am a little confused by how we can consider blue and red parts in series when they are connected by three terminals instead of just one.

 

[erobz]

Interesting approach.

Seems you are splitting as follows

View attachment 333268

and calculating the resistance of the blue part as one thing and then multiplying it by two. I think this multiplication by two is because you are considering the blue in series with the red. Is this so?

I don't see, technically speaking, why you can consider, for example, the left side of the blue part to be 1 + (1 || 1/2) since the wires after the (1 || 1/2) aren't connected together.

This is the same reason why I am a little confused by how we can consider blue and red parts in series when they are connected by three terminals instead of just one.

I believe the line that divides the system in half like that is all at the same potential. It’s effectively a single node.

 

[DaveE]

Interesting approach.

Seems you are splitting as follows

View attachment 333268

and calculating the resistance of the blue part as one thing and then multiplying it by two. I think this multiplication by two is because you are considering the blue in series with the red. Is this so?

I don't see, technically speaking, why you can consider, for example, the left side of the blue part to be 1 + (1 || 1/2) since the wires after the (1 || 1/2) aren't connected together.

This is the same reason why I am a little confused by how we can consider blue and red parts in series when they are connected by three terminals instead of just one.

Because, by symmetry, we know that each node that is midway between the ends must be at equal voltage. If you were to connect those nodes with a wire no current would flow. So the network solution is unchanged by assuming a connection. A wire with no current is the same as no wire.

 

[erobz]

You might consider re-solving this system with loop-mesh and calculating the potentials at the nodes along the black line.

 

[zenterix]

Because, by symmetry, we know that each node that is midway between the ends must be at equal voltage. If you were to connect those nodes with a wire no current would flow. So the network solution is unchanged by assuming a connection. A wire with no current is the same as no wire.

Got it. This is a consequence of symmetry. Indeed, it seems that considering any points in the circuit starting from A, if we consider points with the same proportion of the total resistance between A and B before them (ie between A and them), then those points have the same potential. Half way is the easiest because it is visually easy to see, but if we had chosen 25% (which would mean probably cutting some resistances in two pieces) we could reach the solution in the same way as in the halfway case.

 

[DaveE]

Got it. This is a consequence of symmetry. Indeed, it seems that considering any points in the circuit starting from A, if we consider points with the same proportion of the total resistance between A and B before them (ie between A and them), then those points have the same potential. Half way is the easiest because it is visually easy to see, but if we had chosen 25% (which would mean probably cutting some resistances in two pieces) we could reach the solution in the same way as in the halfway case.

Yes, but 25% is hard because it's asymmetric. So you might have to solve the network first to know where to split the resistors.

 

[alan123hk]

That's it, regardless of whether the red wire connection in the picture below is present or not, the resistance Rab is always equal to 1 ohm. The reason is that the potential of the two points is the same, and no current will flow between the two points after the connection, so the current and potential of the entire circuit do not change.

 

[zenterix]

Yes, but 25% is hard because it's asymmetric. So you might have to solve the network first to know where to split the resistors.

Indeed, just tried it.

The black line would seem at first to be 25% if you just count the number of resistances. But this is incorrect. The equivalent resistance above the black line is 1/3, and this is (1/3)/(4/5) = 5/12 of the total equivalent resistance between A and B. Of course we only know about the 4/5 ex post.

 

[DaveE]

Indeed, just tried it.

View attachment 333277

The black line would seem at first to be 25% if you just count the number of resistances. But this is incorrect. The equivalent resistance above the black line is 1/3, and this is (1/3)/(4/5) = 5/12 of the total equivalent resistance between A and B. Of course we only know about the 4/5 ex post.

But that black line changes the network. Those nodes aren't equipotential with that connection removed.

 

[DaveE]

Again by symmetry the 25% equipotential cut must divide the vertical (central) resistor in half. Using the 50% cut we know the outer half branch has a total resistance of 1+(1||(1/2)) = 4/3. That is cut in half so the upper outer resistor is cut 2/3 of the way down by the 25% equipotential. Without knowing the 50% cut solution by symmetry, I think this is a difficult problem.

 

[alan123hk]

You can also reduce it again with symmetry about the vertical axis which will give you R'=2||(1+1||(1/2))=0.8.
Then the whole network is four R' in a series parallel arrangement so R=R'=0.8.
But I don't think this last step makes the calculation much easier.

Isn't this equivalent to dividing the entire circuit into four parts that are symmetrical up, down, left, and right, with each part accounting for 25%?
So it can be seen almost immediately that the resistance of the entire circuit is 0.8 ohms.

 

[haruspex]

Isn't this equivalent to dividing the entire circuit into four parts that are symmetrical up, down, left, and right, with each part accounting for 25%?
So it can be seen almost immediately that the resistance of the entire circuit is 0.8 ohms.

Very neat, though I don’t understand what you mean by "each part accounting for 25%". Don't you mean each quarter is 0.8Ω, making the whole 0.8Ω?

 

[alan123hk]

I don’t understand what you mean by "each part accounting for 25%". Don't you mean each quarter is 0.8Ω, making the whole 0.8Ω?

Sorry, maybe I said too many unnecessary and useless words.
What I mean is that each part takes up 25% of the visible area of the entire circuit and 25% of the number of parts.

 

[zenterix]

Sorry, maybe I said too many unnecessary and useless words.
What I mean is that each part takes up 25% of the visible area of the entire circuit and 25% of the number of parts.

How would this split be exactly? How woule you split up the resistors on the vertical line in the center running directly from A to B?

 

[zenterix]

But that black line changes the network. Those nodes aren't equipotential with that connection removed.

Indeed the black zig zag line I drew is not of equipotential points. And being equipotential is important if our reasoning is based on putting two pieces of the circuit in series based on those points.

The calculation I did would still be useful I think if for some reason we knew that above the black line was located 5/12 of the total resistance. Because in that case we would know that the equivalent resistance above the line which is 1/3 is 5/12 of the total of the circuit which means that

$$\frac{5}{12}R_{eq,total}=\frac{1}{3}$$

$$R_{eq,total}=\frac{12}{3\cdot 5=\frac{4}{5}}$$

 

[haruspex]

How would this split be exactly? How woule you split up the resistors on the vertical line in the center running directly from A to B?

If you split a resistor R lengthwise, making two parallel resistors, each becomes 2R.
If you split a resistor R crosswise, making two resistors in series, each becomes R/2.

 

[zenterix]

Again by symmetry the 25% equipotential cut must divide the vertical (central) resistor in half. Using the 50% cut we know the outer half branch has a total resistance of 1+(1||(1/2)) = 4/3. That is cut in half so the upper outer resistor is cut 2/3 of the way down by the 25% equipotential. Without knowing the 50% cut solution by symmetry, I think this is a difficult problem.

As you say, calculating the equivalent resistance of the left and right pieces makes it easy to see where we need to split the resistors to have the 25% point.

 

[zenterix]

If you split a resistor R lengthwise, making two parallel resistors, each becomes 2R.
If you split a resistor R crosswise, making two resistors in series, each becomes R/2.

We then have two 4/5 resistors in parallel which gives 2/5 on top. And this is in series with the 2/5 on the bottom so 4/5.

 

[haruspex]

View attachment 333281

We then have two 4/5 resistors in parallel which gives 2/5 on top. And this is in series with the 2/5 on the bottom so 4/5.

Right.

 

[alan123hk]

How would this split be exactly? How woule you split up the resistors on the vertical line in the center running directly from A to B?

The magic diagram symmetrically divides the circuit into four parts.