Finding eigenvector QM 2x2 matrix

[Taylor_1989]

Homework Statement

I am having a issue with how my lecture has normalised the energy state in this question.
I will post my working and I will print screen his solution to the given question below, we have the same answer but I am unsure to why he has used the ratio method.
Q4. a), b), c)

Homework Equations

The Attempt at a Solution

My solution for a), b), c)

a)
$$\hat H|E> = E|E> ;[1]$$

$$\hat H|E> - E|E>=0 ;[2]$$

$$\hat H|E> - IE|E>=0; [3]$$

$$(\hat H-IE)=0 ;[4]$$

$$\begin{pmatrix}0&-\Omega \\ \:-\Omega &\frac{2\Omega }{\sqrt{3}}\end{pmatrix}-E\begin{pmatrix}1&0\\ \:0&1\end{pmatrix}=0 ;[5] $$

So expanding out and finding the determinate of the following matrix

$$\begin{pmatrix}-E&-\Omega \\ \:-\Omega &\frac{2\Omega }{\sqrt{3}}-E\end{pmatrix}=0 ; [6]$$

$$\begin{pmatrix}-E&-\Omega \\ \:-\Omega &\frac{2\Omega }{\sqrt{3}}-E\end{pmatrix}= E^2-\frac{2E\Omega }{\sqrt{3}}-\Omega ^2=0 ;[7]$$

$$\left(E-\frac{3\Omega }{\sqrt{3}}\right)\left(E+\frac{\Omega }{\sqrt{3}}\right)=0 [8]$$

So solving gives me the following for $E_{-}$ and $E_{+}$

$$E_{-}=\frac{3\Omega }{\sqrt{3}} ; [9]$$

$$E_{+}=-\frac{\Omega }{\sqrt{3}} ; [10]$$

b) I solved the eignvector for ground state in the following way

$$\begin{pmatrix}0&-\Omega \\ -\Omega &\frac{2\Omega }{\sqrt{3}}\end{pmatrix}\begin{pmatrix}A\\ B\end{pmatrix}=-\frac{\Omega }{\sqrt{3}}\begin{pmatrix}A\\ B\end{pmatrix} ; [11] $$

$$-\Omega B= -\frac{\Omega }{\sqrt{3}}A ; [12]$$

$$-\Omega A=-\frac{3}{\sqrt{3}}B ; [13]$$

So solving for both of these give $A=\sqrt 3$ so therfore:

$$E_{-}= |0> + \sqrt 3 |1> ; [14]$$

To normalize [14] I found the normalizing constant in the following way:

$$< E_{-} | E_{-} > = 1+3=4 ; [15]$$

$$N^2 < E_{-} | E_{-} > = 1 ; [16]$$

$$N^2=\frac{1}{4}; [17]$$

$$N= \frac{1}{2}; [18]$$

$$|E_{-}> = \frac{1}{2} |0> + \frac{\sqrt 3}{2} | 1 > ; [19]$$

c) $$P(1)=\left(\frac{\sqrt{3}}{2}\right)^2=\frac{3}{4}=75\% [20]$$

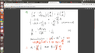
Here is my lecture solution:
a)

b)

last part of b) and all of c)

I just don't understand the ratio method, it is a quicker method than mine or is it used more in more difficult matrices

 

[TSny]

b) I solved the eignvector for ground state in the following way

$$\begin{pmatrix}0&-\Omega \\ -\Omega &\frac{2\Omega }{\sqrt{3}}\end{pmatrix}\begin{pmatrix}A\\ B\end{pmatrix}=-\frac{\Omega }{\sqrt{3}}\begin{pmatrix}A\\ B\end{pmatrix} ; [11] $$

$$-\Omega B= -\frac{\Omega }{\sqrt{3}}A ; [12]$$

$$-\Omega A=-\frac{3}{\sqrt{3}}B ; [13]$$

So solving for both of these give $A=\sqrt 3$

Check your work here. You cannot deduce that $A=\sqrt 3$ from equations [12] and [13]. These equations determine only the ratio of A to B.

So solving for both of these give $A=\sqrt 3$ so therfore:

$$E_{-}= |0> + \sqrt 3 |1> ; [14]$$

It looks like you let $A = 1$ here; whereas, you claimed $A = \sqrt 3$.

In the lecture's solution you find

Check this. The last equation for $\frac{A}{B}$ does not look correct.

 

[Taylor_1989]

Sorry, that was a typo. It is meant to be $A=\sqrt 3 B$ so then I through that as the simplest number for A would be 1 then B would be $\sqrt 3$ time that, so then I got the column vector: $\begin{pmatrix}1\\ \sqrt{3}\end{pmatrix}$. Which the gave me $E_{-} = |0> + \sqrt 3 | 1 >$ and then I normalised

 

[TSny]

It is meant to be $A=\sqrt 3 B$ so then I through that as the simplest number for A would be 1 then B would be $\sqrt 3$ time that, so then I got the column vector: $\begin{pmatrix}1\\ \sqrt{3}\end{pmatrix}$.

If you substitute $A=1$ in the relation $A=\sqrt 3 B$, what do you get for $B$?

 

[Taylor_1989]

Sorry, i will correct this and hopefully will have the correct ans this time. $E_-=\begin{pmatrix}1\\ \frac{1}{\sqrt{3}}\end{pmatrix}$ so then once I have normalized I get the following, $|E_->=\frac{\sqrt{3}}{2}|0>+\frac{1}{2}|1>$ So then my ans for c) would be $25$%. Hopefully this is now correct?

 

[TSny]

$E_-=\begin{pmatrix}1\\ \frac{1}{\sqrt{3}}\end{pmatrix}$ so then once I have normalized I get the following, $|E_->=\frac{\sqrt{3}}{2}|0>+\frac{1}{2}|1>$ So then my ans for c) would be $25$%. Hopefully this is now correct?

Yes, that looks correct.

 

[Taylor_1989]

Ah thank you very much for the help