Find the eigenvalues of a 3x3 matrix

[happyparticle]

Homework Statement

Find the eigenvalues of a 3x3 matrix

Relevant Equations

$\begin{pmatrix} - \omega^2 +\frac{k}{m} &-\frac{k}{m} &0\\ -\frac{k}{M}& - \omega^2 + 2 \frac{k}{M} &-\frac{k}{M} \\ 0&- \frac{k}{m} & -\omega^2 + \frac{k}{m} \end{pmatrix} \begin{pmatrix}A_1\\A_2\\A_3 \end{pmatrix} =0$

Hi,
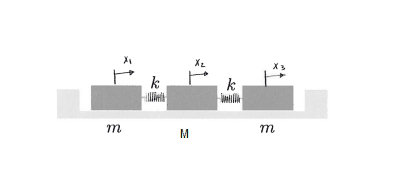
I have a 3 mass system. $M \neq m$

I found the forces and I get the following matrix.

I have to find $\omega_1 , \omega_2, \omega_3$ I know I have to find the values of $\omega$ where det(A) = 0, but with a 3x3 matrix it is a nightmare. I can't find the values.

I'm wondering if there's another way to have the eigenvalues.

$\begin{pmatrix} - \omega^2 +\frac{k}{m} &-\frac{k}{m} &0\\ -\frac{k}{M}& - \omega^2 + 2 \frac{k}{M} &-\frac{k}{M} \\ 0&- \frac{k}{m} & -\omega^2 + \frac{k}{m} \end{pmatrix} \begin{pmatrix}A_1\\A_2\\A_3 \end{pmatrix} =0$

 

[fresh_42]

It is not a nightmare. Set $W=-\omega^2-q-x\, , \,V=W-q\, , \,q=-k/M$ and develop the determinant along the first row. It took me eight lines to find the eigenvalues.

 

[PeroK]

It is not a nightmare.

It's perhaps the sort of thing some people have nightmares about!

 

[happyparticle]

It is not a nightmare. Set $W=-\omega^2-q-x\, , \,V=W-q\, , \,q=-k/M$ and develop the determinant along the first row. It took me eight lines to find the eigenvalues.

I'm not sure to understand the way you set the variables. Why you have $x$ and why not $W = \omega^2 + \frac{k}{m}$

 

[fresh_42]

The eigenvalues are the roots of the polynomial $\det (A-x\cdot I).$ Hence we have $a_{ii}-x$ on the diagonal. You can also work with $W-x$ instead. I simply found it more convenient to calculate $\det\left(\begin{bmatrix} W&q&0\\q&V&q\\0&q&W \end{bmatrix}\right)$ and replace the actual values afterwards rather than
$\det\left(\begin{bmatrix} W-x&q&0\\q&W-q-x&q\\0&q&W-x \end{bmatrix}\right)$. It's a matter of taste.

 

[happyparticle]

You typed $q = \frac{k}{M}$, but you also replaced $\frac{k}{m}$ by q even if $M \neq m$. I don't know if it matters.

At the end I have $VW^2 - \frac{2k^2W}{mM}$ = 0. I didn't replace $\frac{k}{m}$

Using quadratic formula I have $W = 0$ and $W = -4k^2/mM$

then
$-\omega^2 -\frac{k}{m} - x = \frac{-4k^2}{mM}$

It Doesn't give me the right eigenvalues which are, $\omega^2= 0, k/m , k/m + 2k/M$

As usual I probably just don't understood correctly the explanation.

 

[fresh_42]

You have to solve for the determinant $\det(A-xI)$ not just $\det A$.

You typed $q = \frac{k}{M}$, but you also replaced $\frac{k}{m}$ by q even if $M \neq m$. I don't know if it matters.

At the end I have $VW^2 - \frac{2k^2W}{mM}$ = 0. I didn't replace $\frac{k}{m}$

Using quadratic formula I have $W = 0$ and $W = -4k^2/mM$

then
$-\omega^2 -\frac{k}{m} - x = \frac{-4k^2}{mM}$

It Doesn't give me the right eigenvalues which are, $\omega^2= 0, k/m , k/m + 2k/M$

As usual I probably just don't understood correctly the explanation.

You are right. I made a mistake as I used only one mass $M=m$. Sorry.

My corrected result is $\det (A-xI)= \ldots$
$$
0=W(VW-2qQ)=\left(-\omega^2+\dfrac{k}{m}-x\right)\cdot\left(\left(-\omega^2+\dfrac{k}{m}-x\right)\cdot \left(-\omega^2+2\dfrac{k}{M}-x\right)-2\dfrac{k^2}{mM}\right)
$$
which results in $x=-\omega^2+\dfrac{k}{m}$ and the quadratic equation
$$
0=x^2+2x\left(\omega^2-\dfrac{1}{2}\cdot\dfrac{k}{m}-\dfrac{k}{M}\right)+\left(\omega^4-\omega^2\dfrac{k}{m}-2\omega^2\dfrac{k}{M}\right)
$$
which is easy to solve (if I haven't made a mistake again).

In case $\omega$ was your variable, then I do not understand where the square comes from. But then your calculation was correct. I also get $0\, , \,\dfrac{k}{m}\, , \,\dfrac{k}{m}+2\dfrac{k}{M}.$

 

[fresh_42]

I may have misunderstood the problem. You said "I need to find the eigenvalues of a $3\times 3$ matrix" and then came the matrix ... or did you mean I need to solve $\det (A-\omega I)=0$ with eigenvalues $\omega$? I thought it was the first question and then we need a variable, say $x$ for the polynomial. The second possibility has $\omega$ as variable, or $\omega^2$ in your case. But why $\omega^2?$

So what is the matrix you want to find the eigenvalues to?
Or, what is the cubic polynomial you want to find the roots to?

 

[happyparticle]

I may have misunderstood the problem. You said "I need to find the eigenvalues of a $3\times 3$ matrix" and then came the matrix ... or did you mean I need to solve $\det (A-\omega I)=0$ with eigenvalues $\omega$? I thought it was the first question and then we need a variable, say $x$ for the polynomial. The second possibility has $\omega$ as variable, or $\omega^2$ in your case. But why $\omega^2?$

So what is the matrix you want to find the eigenvalues to?
Or, what is the cubic polynomial you want to find the roots to?

Sorry I found my errors. You explanation was perfect. I just didn't realize I don't need to go that far to find the roots for $\omega$

Thanks!