Finding the Speed of a Wedge and Rod System

[Tanya Sharma]

Homework Statement

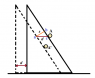
A thin rod of mass m = 1 kg and length l=1m is placed along the hypotenuse side of a wedge lying on a frictionless floor having mass M =5kg and angle 60° . At t= 0 the system is released from rest. Both the objects are free to move .Find the speed of the wedge when the rod makes an angle 30° with the floor.

Homework Equations

The Attempt at a Solution

Let V be the speed of the wedge and v be the speed of the CM of the rod .

Applying conservation of momentum MV = mv_x

Applying energy conservation (mgl/2)(sin60° – sin30°) = (1/2)MV²+ (1/2)mv²+ (1/2)Iω²

Not sure how to proceed. I guess we need to find some constraint relation .

I would be grateful if somebody could help me with the problem.

 

[TSny]

I guess we need to find some constraint relation .

Right.

Hint: The upper end of the rod remains in contact with the surface of the wedge. That should give you a relation between a certain component of the velocity of the wedge and the same component of the velocity of the upper end of the rod.

 

[Tanya Sharma]

Thanks for the response ,TSny .

Component of velocity of the upper end of the rod perpendicular to the hypotenuse face = Vcos30° .

But how do I find the component parallel to the face ? How does that help us in determining the velocity of the CM of the rod ? I guess I need to find the x-component of velocity of CM of the rod .

 

[TSny]

Component of velocity of the upper end of the rod perpendicular to the hypotenuse face = Vcos30° .

Good.

But how do I find the component parallel to the face ? How does that help us in determining the velocity of the CM of the rod ? I guess I need to find the x-component of velocity of CM of the rod .

I'm not sure you need to find the component parallel to the face. But you do have a second constraint at the lower end of the rod that you can use.

 

[Satvik Pandey]

Homework Statement

Let V be the speed of the wedge and v be the speed of the CM of the rod .

Applying conservation of momentum MV = mv_x...(1)

Applying energy conservation (mgl/2)(sin60° – sin30°) = (1/2)MV²+ (1/2)mv²+ (1/2)Iω² ...(2)

.

Sorry for interrupting in between.
I understood the first equation.I have also understood LHS of eq(2) but I am not able to understand why you have used expression \frac{Iω}{2} here.
The rod is not rotating here I think.

 

[TSny]

The rod is not rotating here I think.

The angle that the rod makes to the horizontal continually decreases until the rod becomes horizontal when it hits the floor. So, at the instant the rod makes a 30^o angle, the rod is rotating.

 

[Tanya Sharma]

I'm not sure you need to find the component parallel to the face. But you do have a second constraint at the lower end of the rod that you can use.

I have thought about it but not sure how we would use the constraint at the lower end . Does this help us in determining the velocity of the CM or the angular velocity of the rod ?

 

[Satvik Pandey]

Right.

Hint: The upper end of the rod remains in contact with the surface of the wedge. That should give you a relation between a certain component of the velocity of the wedge and the same component of the velocity of the upper end of the rod.

The velocities of wedge and rod perpendicular to the to the contact surface should be same.
So Vcos60=vcos30
Is it right?

 

[TSny]

I have thought about it but not sure how we would use the constraint at the lower end . Does this help us in determining the velocity of the CM or the angular velocity of the rod ?

Can you use the constraint at the lower end of the rod to help you express the y-component of the CM in terms of ω? It is helpful to remember the relative velocity formula $\vec{V}_A = \vec{V}_C + \vec{V}_{A/C}$ for any two points A and C of the rod. Think about the points you might choose for A and C.

 

[Tanya Sharma]

Can you use the constraint at the lower end of the rod to help you express the y-component of the CM in terms of ω?

Yes.

It is helpful to remember the relative velocity formula $\vec{V}_A = \vec{V}_C + \vec{V}_{A/C}$ for any two points A and C of the rod. Think about the points you might choose for A and C.

If I consider the upper end of the rod and the Center then the only useful information we have is the component of velocity of upper end perpendicular to the face of the wedge .

Also , not sure how the component of velocity of the upper end we have calculated is useful for us ?

 

[TSny]

If I consider the upper end of the rod and the Center then the only useful information we have is the component of velocity of upper end perpendicular to the face of the wedge .

Also , not sure how the component of velocity of the upper end we have calculated is useful for us ?

Combine these. That is, if you let A be the upper end of the rod and C be the CM, what do you get if you combine $\vec{V}_A = \vec{V}_C + \vec{V}_{A/C}$ and the constraint equation for A?

 

[Tanya Sharma]

$\vec{V}_A = (\frac{M}{m}V+\frac{l}{2}ωsinθ)\hat{i}$

Is it correct ?

 

[TSny]

$\vec{V}_A = (\frac{M}{m}V+\frac{l}{2}ωsinθ)\hat{i}$

Is it correct ?

$\vec{V}_A$ should have both x and y components. Are you taking $\hat{i}$ to point to the right?

We've got a lot of variables. For now, just express the Cartesian components of $\vec{V}_C$ as $v_x$ and $v_y$. Express the Cartesian components of $\vec{V}_{A/C}$ in terms of $\omega$ and $\theta$. Then you can express $\vec{V}_A$ in terms of $v_x$ , $v_y$ , $\omega$ and $\theta$.

 

[Tanya Sharma]

$\vec{V}_A$ should have both x and y components. Are you taking $\hat{i}$ to point to the right?

$\hat{i}$ to the right and $\hat{j}$ upwards .

$\vec{V}_C = \frac{M}{m}V\hat{i} + \frac{l}{2}ωcosθ\hat{j}$

$\vec{V}_{A/C} = \frac{l}{2}ωsinθ\hat{i} + \frac{l}{2}ωcosθ\hat{j}$

 

[TSny]

$\hat{i}$ to the right and $\hat{j}$ upwards .

$\vec{V}_C = \frac{M}{m}V\hat{i} + \frac{l}{2}ωcosθ\hat{j}$

$\vec{V}_{A/C} = \frac{l}{2}ωsinθ\hat{i} + \frac{l}{2}ωcosθ\hat{j}$

Close. But I think there are several sign errors. Does the CM have an upward y-component of velocity? Reconsider the direction of $\vec{V}_{A/C}$.

 

[Tanya Sharma]

Doesn't the negative value of ω make the y-component of velocity negative ?

 

[TSny]

OK. I didn't notice that you were taking clockwise as positive rotation.

[But it seems less confusing to me to take CCW as positive rotation for this problem.]

 

[Tanya Sharma]

OK. I didn't notice that you were taking clockwise as positive rotation

So, post#14 okay ?

[But it seems less confusing to me to take CCW as positive rotation for this problem.]

But the angle which the rod makes with the horizontal , automatically makes CW positive ?

 

[TSny]

Yes, post 14 is OK with ω a negative number.

I was considering ω as just the angular velocity of the rod in the CCW direction, rather than defining it as ω = dθ/dt. But, your way is good.

 

[Tanya Sharma]

So , $\vec{V}_A = (\frac{M}{m}V+\frac{l}{2}ωsinθ)\hat{i} + lωcosθ\hat{j}$

Here y-component is negative .

But how do I determine whether the x-component is positive or negative , because that will determine the angle which the x-component makes with the direction perpendicular to hypotenuse face ?

Edit : I am trying to find the component of these components in the direction perpendicular to the face .

 

[TSny]

So , $\vec{V}_A = (\frac{M}{m}V+\frac{l}{2}ωsinθ)\hat{i} + lωcosθ\hat{j}$

Here y-component is negative .

But how do I determine whether the x-component is positive or negative , because that will determine the angle which the components make with the direction perpendicular to hypotenuse face ?

Edit : I am trying to find the component of these components in the direction perpendicular to the face .

You now have $\vec{V}_A = V_{Ax}\hat{i} + V_{Ay}\hat{j}$ with explicit expressions for $V_{Ax}$ and $V_{Ay}$.

You need to consider the component of $\hat{i}$ perpendicular to the wedge and likewise for $\hat{j}$. The coefficients of $\hat{i}$ and $\hat{j}$ will just go along with the ride no matter what their signs.

 

[Tanya Sharma]

Do you agree that $\hat{i}$ makes angle 150° with the perpendicular to the wedge (pointing inwards) and $\hat{j}$ makes angle 120° ?

 

[TSny]

Do you agree that $\hat{i}$ makes angle 150° with the perpendicular to the wedge (pointing inwards) and $\hat{j}$ makes angle 120° ?

Yes.

 

[Tanya Sharma]

Are you getting $$\sqrt{\frac{15\sqrt{3}-1}{142}}$$

 

[TSny]

Are you getting $$\sqrt{\frac{15\sqrt{3}-1}{142}}$$

Almost. Did you leave out parentheses in the numerator? And I assume you're taking g = 10.

 

[Tanya Sharma]

Yes . Assuming g=10 , $$ \sqrt{\frac{15(\sqrt{3}-1)}{142}} $$

 

[TSny]

Yes. That's what I got, too.

 

[Tanya Sharma]

Cheers

Thank you so much . I could not have solved it without your guidance .

 

[Satvik Pandey]

The angle that the rod makes to the horizontal continually decreases until the rod becomes horizontal when it hits the floor. So, at the instant the rod makes a 30^o angle, the rod is rotating.

Could you please tell me around which axis is it rotating?
Sorry for interrupting again.

 

[Nathanael]

Could you please tell me around which axis is it rotating?

The axis of rotation is perpendicular to the page.


If you mean exactly where is the axis located? I think there are several correct ways to look at it.

For example, you could look at it as rotation about the (rod's) center of mass, (although the center of mass moving vertically and horizontally)

Another way is to look at it as rotation about the end of the rod that is touching the floor
(I think this way is more simple, because this way the rotation axis is only moving horizontally, not vertically)


There are other ways too, and if I'm not mistaken, all of them are valid (although some are more simple than others)

 

[Satvik Pandey]

The axis of rotation is perpendicular to the page.


If you mean exactly where is the axis located? I think there are several correct ways to look at it.

For example, you could look at it as rotation about the (rod's) center of mass, (although the center of mass moving vertically and horizontally)

Another way is to look at it as rotation about the end of the rod that is touching the floor
(I think this way is more simple, because this way the rotation axis is only moving horizontally, not vertically)


There are other ways too, and if I'm not mistaken, all of them are valid (although some are more simple than others)

Thank you Nathanael.
This is the case in which rod is going through translation and rotational motion simultaneously.
Is it so?

 

[Satvik Pandey]

Thanks for the response ,TSny .

Component of velocity of the upper end of the rod perpendicular to the hypotenuse face = Vcos30° .
.

I am unable to understand why velocity of the upper end of the rod perpendicular to the hypotenuse face = Vcos30° .It would be nice if you could help.
From this figure

h^{2}= p^{2}+ b^{2}
differentiating the above equation with respect to time we get
0=2p\frac{dp}{dt}+ 2b \frac{db}{dt}
0=2pv'+2bv
-\frac{b}{p}v=v'
-cot θv=v'
Component of this velocity perpendicular to h=v'cosθ
=-cotθvcosθ but this is not what you have found.

 

[TSny]

I am unable to understand why velocity of the upper end of the rod perpendicular to the hypotenuse face = Vcos30°.

See the attached figure. The points A and A’ represent the initial and final locations of the upper end of the rod as the wedge moves horizontally to the left by a small distance d. The distance s is the distance that the upper end of the rod moves perpendicularly to the hypotenuse of the wedge. Using trig on triangle abc, what is the relationship between s and d?

 

[Satvik Pandey]

See the attached figure. The points A and A’ represent the initial and final locations of the upper end of the rod as the wedge moves horizontally to the left by a small distance d. The distance s is the distance that the upper end of the rod moves perpendicularly to the hypotenuse of the wedge. Using trig on triangle abc, what is the relationship between s and d?

Is it \frac{s}{d}=cos(30)

 

[TSny]

Is it \frac{s}{d}=cos(30)

Yes. From that you should be able to show that the velocity of the upper end of the rod has a component perpendicular to the wedge hypotenuse equal to Vcos(30), where V is the velocity of the wedge.

 

[Satvik Pandey]

Yes. From that you should be able to show that the velocity of the upper end of the rod has a component perpendicular to the wedge hypotenuse equal to Vcos(30), where V is the velocity of the wedge.

So s=dcos(30)

\frac{ds}{dt}=\frac{ddcos(30)}{dt}
As θ is not going to vary with time.
So \frac{ds}{dt}=\frac{dd}{dt}cos(30)

\frac{ds}{dt}=Vcos(30).

Thank you TSny.

 

[Satvik Pandey]

$\hat{i}$ to the right and $\hat{j}$ upwards .

$\vec{V}_C = \frac{M}{m}V\hat{i} + \frac{l}{2}ωcosθ\hat{j}$

$\vec{V}_{A/C} = \frac{l}{2}ωsinθ\hat{i} + \frac{l}{2}ωcosθ\hat{j}$

I was unable to understand how you find V_{C}and V_{A/C}
I tried to understand your solution but it is a bit difficult.I tried this.
Let the rod rotate along CM
So,Vcosθ=lω/2
velocity of this component in y direction=lωcosθ/2
So V_{A}=-MV/m$\hat{i}$-lωcosθ$\hat{j}$
Is it right?I also have some sign error. I am unable to find V_{A/C}?










-

 

[Satvik Pandey]

I was unable to understand how you find V_{C}and V_{A/C}
I tried to understand your solution but it is a bit difficult.I tried this.
Let the rod rotate along CM
So,Vcosθ=lω/2
velocity of this component in y direction=lωcosθ/2
So V_{A}=-MV/m$\hat{i}$-lωcosθ$\hat{j}$
Is it right?I also have some sign error. I am unable to find V_{A/C}?-

Here is the figure.

 

[TSny]

I was unable to understand how you find V_{C}and V_{A/C}
I tried to understand your solution but it is a bit difficult.I tried this.
Let the rod rotate along CM
So,Vcosθ=lω/2
velocity of this component in y direction=lωcosθ/2
So V_{A}=-MV/m$\hat{i}$-lωcosθ$\hat{j}$
Is it right?I also have some sign error. I am unable to find V_{A/C}?

Your y component of V_{A} looks correct if ω represents the magnitude of the angular velocity (i.e., a positive number). However, the x-component is not correct. The equation Vcosθ=lω/2 is also not correct.

We have the relative velocity formulas $$\vec{V}_A = \vec{V}_C + \vec{V}_{A/C}$$ $$\vec{V}_B = \vec{V}_C + \vec{V}_{B/C}$$ where A is the upper end of the rod, B is the lower end of the rod, and C is the center of mass of the rod. See the attached figure.

Can you express the magnitudes of $\vec{V}_{A/C}$ and $\vec{V}_{B/C}$ in terms of $\omega$?

 

[Satvik Pandey]

Your y component of V_{A} looks correct if ω represents the magnitude of the angular velocity (i.e., a positive number). However, the x-component is not correct. The equation Vcosθ=lω/2 is also not correct.

We have the relative velocity formulas $$\vec{V}_A = \vec{V}_C + \vec{V}_{A/C}$$ $$\vec{V}_B = \vec{V}_C + \vec{V}_{B/C}$$ where A is the upper end of the rod, B is the lower end of the rod, and C is the center of mass of the rod. See the attached figure.

Can you express the magnitudes of $\vec{V}_{A/C}$ and $\vec{V}_{B/C}$ in terms of $\omega$?

If the rod rotates around the CM of the rod then by v=rω
V_{A/C}=lω/2 (Considering CCW as +ve)
V_{B/C}=-lω/2
But how can we say that directions of V_A/c and V_B/C are perpendicular to the rod(from figure in#39) ?
It seems to be correct but are there any proofs.

 

[TSny]

Relative to C, all the points of the rod move in circles around C. The velocity of a point moving in a circle is tangent to the circle, and therefore perpendicular to the radius of the circle.

Yes, the magnitudes of $V_{A/C}$ and $V_{B/C}$ are each equal to $l\omega/2$.

Can you express the x and y components of $\vec{V}_{A/C}$ and $\vec{V}_{B/C}$ in terms of $l$, $\omega$ and $\theta$?

 

[Satvik Pandey]

Relative to C, all the points of the rod move in circles around C. The velocity of a point moving in a circle is tangent to the circle, and therefore perpendicular to the radius of the circle.

OK got it.
THANK YOU FOR HELP.

 

[Satvik Pandey]

Relative to C, all the points of the rod move in circles around C. The velocity of a point moving in a circle is tangent to the circle, and therefore perpendicular to the radius of the circle.

Yes, the magnitudes of $V_{A/C}$ and $V_{B/C}$ are each equal to $l\omega/2$.

Can you express the x and y components of $\vec{V}_{A/C}$ and $\vec{V}_{B/C}$ in terms of $l$, $\omega$ and $\theta$?

V_A/C=-lωsinθ/2 \hat{i}-lωcosθ/2 \hat{j}
V_B/C=-lωsinθ/2 \hat{i}-lωcosθ/2 \hat{j}

i hat +ve towards right and j hat +ve in upward direction.

 

[TSny]

OK for $\vec{V}_{A/C}$, but the signs are wrong for $\vec{V}_{B/C}$. (I'm assuming $\omega$ is a positive number.)

 

[Satvik Pandey]

OK for $\vec{V}_{A/C}$, but the signs are wrong for $\vec{V}_{B/C}$. (I'm assuming $\omega$ is a positive number.)

Yes there should be +ve sign instead of -ve sign.

V_{B/C}=lωsinθ/2 \hat{i}+lωcosθ/2\hat{j}

 

[Satvik Pandey]

I tried to find V_C.
As V_C/B=V_C-V_B
V_{C}=V_{C/B}+V_{B}

V_{C/B}=-lωsinθ/2\hat{i} -lωcosθ/2\hat{j}.V_{B}=MV/m \hat{i}
Comb. these

V_{C}=-lωsinθ/2\hat{i} -lωcosθ/2\hat{j}+MV/m \hat{i}
Is it right?

I have considered ω here w.r.t axis passing through B.
Will it be same as ω w.r.t axis passing through C which I have used earlier?

 

[TSny]

V_{B}=MV/m \hat{i}

This equation isn't correct.

The idea is to use the energy equation to solve for the speed of the wedge, V. The energy equation contains V as well as the speed of the center of mass of the rod, V_C, and the angular speed of the rod, ω. So, we need to express V_C and ω in terms of V.

Using conservation of momentum in the x-direction, what can you deduce about the x component of $\vec{V}_C$?

To get some information about the y-component of $\vec{V}_C$, what do you get if you take the y-component of the equation $\vec{V}_B = \vec{V}_C + \vec{V}_{B/C}$?

 

[Satvik Pandey]

This equation isn't correct.

The idea is to use the energy equation to solve for the speed of the wedge, V. The energy equation contains V as well as the speed of the center of mass of the rod, V_C, and the angular speed of the rod, ω. So, we need to express V_C and ω in terms of V.

Using conservation of momentum in the x-direction, what can you deduce about the x component of $\vec{V}_C$?

To get some information about the y-component of $\vec{V}_C$, what do you get if you take the y-component of the equation $\vec{V}_B = \vec{V}_C + \vec{V}_{B/C}$?

THANK YOU TSny.
By conservation of momentum where v_{x} is the velocity of CM (x-comp.)
MV=mv_{x}

v_{x}=MV/m

$\vec{V}_B = \vec{V}_C + \vec{V}_{B/C}$
0=V_{C}+\frac{lωcosθ}{2} \hat{j}

V_{C}=-\frac{lωcosθ}{2} \hat{j}

V_{C}=\frac{MV}{m}\hat{i}-\frac{lωcosθ}{2} \hat{j}
Is it right?

 

[Satvik Pandey]

V_A=V_C+V_A/C

V_A={\frac{MV}{m}-\frac{-lωsinθ}{2}}\hat{i} -lωcosθ/2\hat{j}.
Is it right?
What to do next?

 

[TSny]

THANK YOU TSny.
By conservation of momentum where v_{x} is the velocity of CM (x-comp.)
MV=mv_{x}

v_{x}=MV/m

$\vec{V}_B = \vec{V}_C + \vec{V}_{B/C}$
0=V_{C}+\frac{lωcosθ}{2} \hat{j}

V_{C}=-\frac{lωcosθ}{2} \hat{j}

V_{C}=\frac{MV}{m}\hat{i}-\frac{lωcosθ}{2} \hat{j}
Is it right?

Looks good.