- #1
Apashanka
- 429
- 15
If considering the 4-D manifold(##x^1,x^2,x^3,t##) in which the sub-manifold dimensionality is 3(##x^1,x^2,x^3##)(hypersurface)
We are writting the metric of this space as ##ds^2=g(t)dt^2+f(t)\gamma_{ij}{dx^idx^j}\delta_{ij}## where the term ##\gamma_{ij}dx^idx^j\delta_{ij}## is the metric of the hypersurface assuming that ##\frac{∂}{∂t}=\hat t## is orthogonal to the hypersurface .
A very elementary rough diagram is this
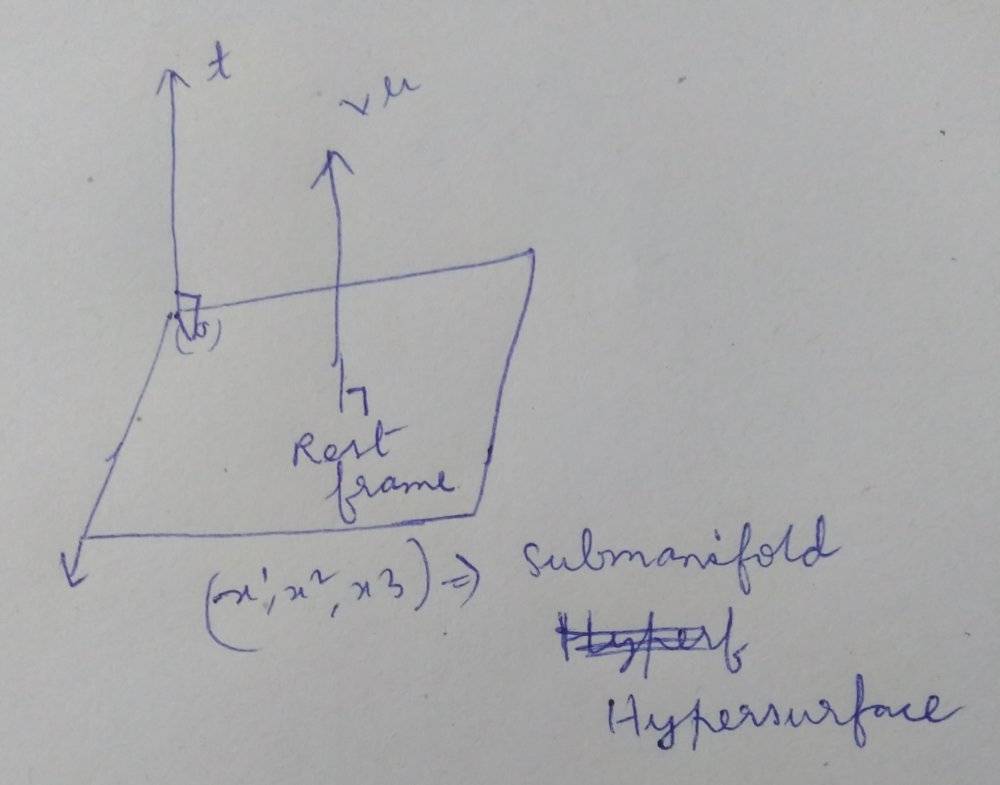
Now from the four velocity ##V^\mu=\gamma##{c,##v_{spatial}##}
If a particle is at rest in one frame then it's ##V^\mu## points along ##\hat t## (perpendicular to the hypersurface) and if it is having some spatial velocity in another frame then the velocity four vector ##V^\mu## is now tilted at an angle to the hypersurface(e.g roughly we can say there are two components ,along ##\hat t## and ##V_{hypersurface})##
Till now it's ok but these lines from a paper I am unable to understand and connects ,to the above

From ''Accordingly .....to ##b_{\mu \nu}##'' here ##n## is along ##\hat t## and ##u## is the four velocity.
Can anyone help me in sort out this
We are writting the metric of this space as ##ds^2=g(t)dt^2+f(t)\gamma_{ij}{dx^idx^j}\delta_{ij}## where the term ##\gamma_{ij}dx^idx^j\delta_{ij}## is the metric of the hypersurface assuming that ##\frac{∂}{∂t}=\hat t## is orthogonal to the hypersurface .
A very elementary rough diagram is this
Now from the four velocity ##V^\mu=\gamma##{c,##v_{spatial}##}
If a particle is at rest in one frame then it's ##V^\mu## points along ##\hat t## (perpendicular to the hypersurface) and if it is having some spatial velocity in another frame then the velocity four vector ##V^\mu## is now tilted at an angle to the hypersurface(e.g roughly we can say there are two components ,along ##\hat t## and ##V_{hypersurface})##
Till now it's ok but these lines from a paper I am unable to understand and connects ,to the above
From ''Accordingly .....to ##b_{\mu \nu}##'' here ##n## is along ##\hat t## and ##u## is the four velocity.
Can anyone help me in sort out this
