Hash marks on minkowski diagram

[idea2000]

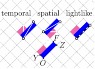
I'm confused as to how far apart the hash marks should be on a minkowski spacetime diagram that shows the rocket frame overlapped over the lab frame. Should the hash marks that represent space in the rocket frame be spaced apart exactly the same length as the hash marks that represent space in the lab frame? How do we go about determining how far apart the hash marks should be? Do we just rotate the x-axis to get the x' axis and keep the hash marks space the same length apart? Any help would be greatly appreciated. Thanks in advance!

 

[Orodruin]

Just like the circle $x^2+y^2 = 1$ intersects the x and y axes in Euclidean space at x=1 and y=1, respectively, the hyperbola $(ct)^2 - x^2 = 1$ intersects the t axis at ct=1 and $(ct)^2-x^2=-1$ intersects the x-axis at x=1. Since $(ct)^2-x^2$ is Lorentz invariant, this is true also for the t’ and x’ coordinates. To mark the units on a Minkowski diagram, you therefore draw these hypernolae and see where they intersect your axes. That position is the unit mark. You then make additional equidistant marks based on the distance to the origin.

 

[idea2000]

I'm having some trouble visualizing what you are saying. =) In general, are the hash marks in the rocket frame going to spaced farther apart than in the lab frame?

 

[idea2000]

If the proper time is 1, then every solution to (ct)^2 - x^2 = 1 represents a what a different frame sees. Does each (x,ct) solution represent a hash mark on a specific rocket frame?

 

[robphy]

Have a look at my PF Insights
https://www.physicsforums.com/insights/spacetime-diagrams-light-clocks/
https://www.physicsforums.com/insights/relativity-rotated-graph-paper/

The diagonals of an observer's light-clock diamonds mark off the tickmarks along an observer's time and space axes.
The area of these diamonds is a Lorentz invariant. Under a boost, the light-like directions are preserved and (since the determinant equals one) the area is preserved. The stretching and shrinking along the light-like directions are the Doppler factors (the eigenvalues of the boost).

 

[idea2000]

I see, the pictures were very helpful. Thanks!

 

[idea2000]

I had one more question about symmetry. If the laboratory frame sees the rocket frame's hash marks as being spaced wider apart, does that mean that the rocket frame would also see the laboratory frame's hash marks as being spaced wider apart as well? In other words, if we were to redraw the whole diagram from the rocket frame, would the laboratory frame's hash marks be wider apart?

 

[robphy]

Yes.

 

[vanhees71]

Just like the circle $x^2+y^2 = 1$ intersects the x and y axes in Euclidean space at x=1 and y=1, respectively, the hyperbola $(ct)^2 - x^2 = 1$ intersects the t axis at ct=1 and $(ct)^2-x^2=-1$ intersects the x-axis at x=1. Since $(ct)^2-x^2$ is Lorentz invariant, this is true also for the t’ and x’ coordinates. To mark the units on a Minkowski diagram, you therefore draw these hypernolae and see where they intersect your axes. That position is the unit mark. You then make additional equidistant marks based on the distance to the origin.

For a graphical illustration of this very straight-forward way to explain the right "scaling" of the axes of different inertial observers, see Fig. 1.1 on p9 of

https://th.physik.uni-frankfurt.de/~hees/pf-faq/srt.pdf

One should clarify this issue by the clear statement that you must forget your Euclidean geometry of the plane completely and substitute it by Minkowskian geometry, where indeed the "unit circles" must be substituted by the unit hyperbolae $(c t)^2-x^2=\pm 1$ of constant unit proper time or unit distance, respectively.

For an alternative depiction of space time, based on the use of "light-cone coordinates", see @robphy 's Insight articles, quoted in #5.