- #1
Math Amateur
Gold Member
MHB
- 3,992
- 48
I am reading James Munkres' book, Elements of Algebraic Topology.
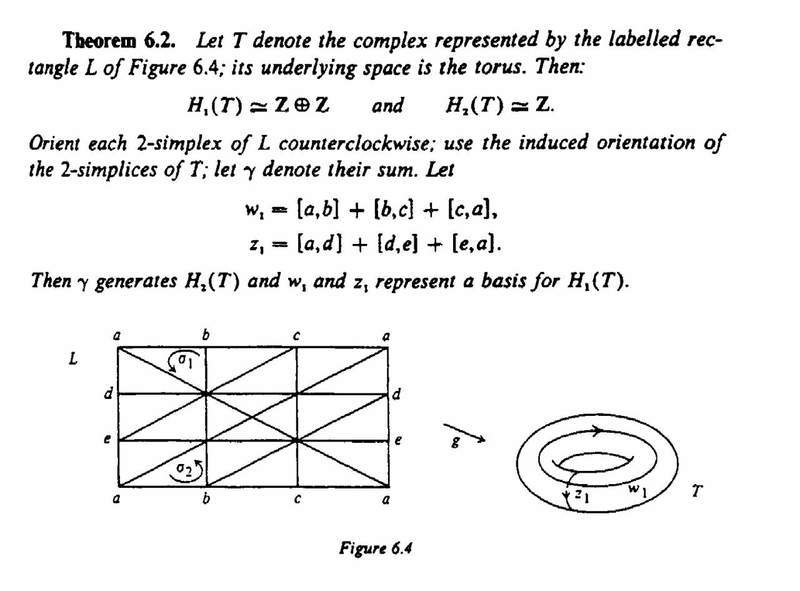
Theorem 6.2 on page 35 concerns the homology groups of the 2-dimensional torus.
Munkres shows that [itex] H_1 (T) \simeq \mathbb{Z} \oplus \mathbb{Z} [/itex] and [itex] H_2 (T) \simeq \mathbb{Z} [/itex].
After some work I now (just!) follow the proof that [itex] H_1 (T) \simeq \mathbb{Z} \oplus \mathbb{Z} [/itex] but I need some help to understand a point in the proof of [itex] H_2 (T) \simeq \mathbb{Z} [/itex].
Munkres' argument to show [itex] H_2 (T) \simeq \mathbb{Z} [/itex] is as follows:
-----------------------------------------------------------------------------
To compute [itex] H_2 (T) [/itex], note that by (2) any 2-cycle d of T must be of the form [itex] p \gamma [/itex] for some p. Each such 2-chain is in fact a cycle,by (4) , and there are no 3-chains for it to bound. We conclude that
[itex] H_2 (T) \simeq \mathbb{Z} [/itex]
and this group has as generator the 2-cycle [itex] \gamma [/itex].
------------------------------------------------------------------------------------------------
I do not fully understand why any 2-cycle d of T must be of the form [TEX] p \gamma [/TEX] for some p.
Can someone please explain exactly why this follows?
Would appreciate some help.
-----------------------------------------------------------------------------
To give members of the Physics Forums the context of the post above, the text of Theorem 6.2 and its proof follow:

Some of my thoughts ... ...
Basically, to show that any 2-cyclce of L (i.e. T) os of the form \(\displaystyle p \gamma \), we have to show the following:
If [itex] d = \sum_i n_i \sigma_i [/itex] where [itex] \partial d = 0 [/itex] then [itex] d = p \gamma [/itex].
We have, of course that [itex] \gamma = \sum_i \sigma_i [/itex]
Note that we have that if d is a 2-chain of L and if [itex] \partial d [/itex] is carried by A then d is a multiple of [itex] \gamma [/itex].
Munkres defines 'carried by' in the following text taken from page 31:
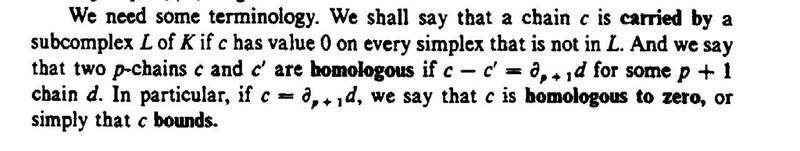
Hope someone can help.
Peter
Theorem 6.2 on page 35 concerns the homology groups of the 2-dimensional torus.
Munkres shows that [itex] H_1 (T) \simeq \mathbb{Z} \oplus \mathbb{Z} [/itex] and [itex] H_2 (T) \simeq \mathbb{Z} [/itex].
After some work I now (just!) follow the proof that [itex] H_1 (T) \simeq \mathbb{Z} \oplus \mathbb{Z} [/itex] but I need some help to understand a point in the proof of [itex] H_2 (T) \simeq \mathbb{Z} [/itex].
Munkres' argument to show [itex] H_2 (T) \simeq \mathbb{Z} [/itex] is as follows:
-----------------------------------------------------------------------------
To compute [itex] H_2 (T) [/itex], note that by (2) any 2-cycle d of T must be of the form [itex] p \gamma [/itex] for some p. Each such 2-chain is in fact a cycle,by (4) , and there are no 3-chains for it to bound. We conclude that
[itex] H_2 (T) \simeq \mathbb{Z} [/itex]
and this group has as generator the 2-cycle [itex] \gamma [/itex].
------------------------------------------------------------------------------------------------
I do not fully understand why any 2-cycle d of T must be of the form [TEX] p \gamma [/TEX] for some p.
Can someone please explain exactly why this follows?
Would appreciate some help.
-----------------------------------------------------------------------------
To give members of the Physics Forums the context of the post above, the text of Theorem 6.2 and its proof follow:
Some of my thoughts ... ...
Basically, to show that any 2-cyclce of L (i.e. T) os of the form \(\displaystyle p \gamma \), we have to show the following:
If [itex] d = \sum_i n_i \sigma_i [/itex] where [itex] \partial d = 0 [/itex] then [itex] d = p \gamma [/itex].
We have, of course that [itex] \gamma = \sum_i \sigma_i [/itex]
Note that we have that if d is a 2-chain of L and if [itex] \partial d [/itex] is carried by A then d is a multiple of [itex] \gamma [/itex].
Munkres defines 'carried by' in the following text taken from page 31:
Hope someone can help.
Peter
Attachments
-
 Theorem 6.2 - Part 1 - Page 35 - Munkres - Elements of Algebraic Topology.jpg40.6 KB · Views: 719
Theorem 6.2 - Part 1 - Page 35 - Munkres - Elements of Algebraic Topology.jpg40.6 KB · Views: 719 -
 Theorem 6.2 - Part 2 - Page 35 - Munkres - Elements of Algebraic Topology.jpg62.2 KB · Views: 674
Theorem 6.2 - Part 2 - Page 35 - Munkres - Elements of Algebraic Topology.jpg62.2 KB · Views: 674 -
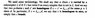 Definition of Carried By and Homologous - Munkres page 31 - Elements of Algebraic Topology.jpg21.1 KB · Views: 638
Definition of Carried By and Homologous - Munkres page 31 - Elements of Algebraic Topology.jpg21.1 KB · Views: 638
Last edited: