How is the direction of a harmonic wave expressed?

[WickedSymphony]

TL;DR Summary

Why is a backwards traveling wave expressed as exp[i (kx + wt) ] instead of exp[ i ( -kx -wt ) ], since k is the term that carries directional information?

I've been having an issue with understanding the convention of wave direction notation, here is my current understanding where I am at currently:

A 3D harmonic solution to the differential wave equation can be given as:

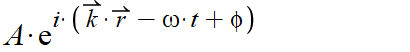
If we make some assumptions about the wave, that its amplitude is 1, its traveling along the positive x-axis, and that the phase shift is 0, we get the 1D wave equation traveling along the x-axis.

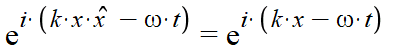
Up until this point I feel as though my understanding is fine. However, when I try to describe a wave that's identical to this one except traveling in the opposite direction is where I get confused. From both some classes I've taken and things I've read, an often used convention for describing a wave traveling backwards is:

And to me this doesn't make sense. If I'm not mistaken (which I very well might be) the frequency of a wave isn't negative, its always greater than 0, and time is not running backwards. So I don't understand why the w*t term would change sign. In my mind since the propagation vector, k, is the term that carries direction, it should be what becomes negative in the expression. So I think the (or an) expression "should" be:

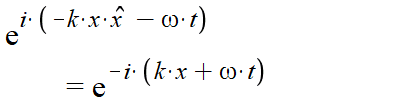
and

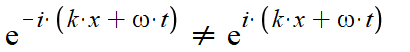
So there is clearly a difference between the convention I've been taught and read about, and the expression that, to me at the very least, seems like it should be the proper one.

One thing I've noticed, is that if you use euler's formula on both of these expressions, and then use the even and oddness of the cosine and sine functions you get:

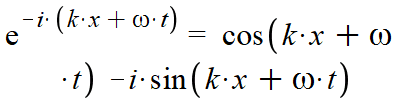
and

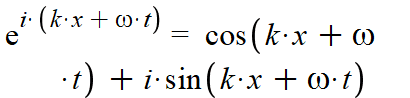
Which have the same real part but different imaginary parts. Often times the real part of the wave is the only part that we care about, in which case the conventional method and "my" method actually agree. However, if I am not mistaken the imaginary part of the expression actually carries information about the phase of the wave, so may indicate that there's only a phase difference between the 2 expressions. That said, since they are both trying to describe the same wave, they should have the same phase.

If anyone could lend insight into this issue, as to where I may have gone wrong or to a convention issue or anything else I may have missed it would be much appreciated.

 

[robphy]

Consider the phase $\theta_0$ at a given $(x_0,t_0)$. ($k>0, \omega >0$)
To keep the same phase [and, thus, disturbance from equilibrium] with $\theta_0= ( kx-\omega t)$,
as t increases, what must $x$ do to keep the same phase?

Try again with $(kx+\omega t)$.

 

[kuruman]

Not to mention that the argument of a sinusoidal is a scalar not a vector and as such it cannot indicate direction. As @robphy pointed out, direction is implied by whether a contant phase increases or decreases as time increases (which time always does).

 

[WickedSymphony]

Consider the phase $\theta_0$ at a given $(x_0,t_0)$. ($k>0, \omega >0$)
To keep the same phase [and, thus, disturbance from equilibrium] with $\theta_0= ( kx-\omega t)$,
as t increases, what must $x$ do to keep the same phase?

Try again with $(kx+\omega t)$.

Ok,

for $( kx - \omega t ) = \theta_0$
the x as a function of t will be $\frac { \omega t + \theta_0} {k}$ so as time goes up x will increase at a rate of $\frac \omega k$ which means x will move in the positive direction. As for $( kx + \omega t ) = \theta_0$ , x as a function of t will be $\frac {- \omega t + \theta_0} {k}$ so as t increases x will change at a rate of $\frac {-\omega} k$ meaning it will be going backwards. So that all makes sense, and I can see why the conventional description works.

If I try the same thing on the other form by taking the propagation vector k to be in the $- \hat x$ direction i get ## ## $( -kx - \omega t ) = \theta_0$ then x as a function of t will be $- \frac {\omega t + \theta_0} {k}$ this form also has x decrease as t increases, showing it will travel backwards, and it seems it will also travel backwards at the same rate as the other form. That said there seems to be a phase difference, which coincidentally confirmed what I suspected looking at euler's formulas. Why would there be this phase difference?

 

[WickedSymphony]

Not to mention that the argument of a sinusoidal is a scalar not a vector and as such it cannot indicate direction. As @robphy pointed out, direction is implied by whether a contant phase increases or decreases as time increases (which time always does).

The argument in the sinusoid has to be a scalar, but we know that the dot product of 2 vectors ( in this case the propagation vector and position vector) returns a scalar. So can't the scalar value that is the argument of the sinusoid be vector dependent? For example one of the recent things I've read to try and gain insight on my own is: http://www.physics.usu.edu/riffe/3750/Lecture 18.pdf , which describes a 3D wave as $Ae^{i( \vec k \cdot \vec r - \omega t)}$ So $\vec r$ is an arbitrary position in space that we want to look at, but $\vec k$ is the wave specific vector quantity indicating the wavenumber, $|\vec k |$, and propagation direction, $\hat k$ . And since if were talking about 2 waves that only differ by direction, shouldn't one wave be $Ae^{ i(|\vec k| \hat k \cdot \vec r - \omega t) }$ and the other wave be $Ae^{ i(|\vec k| -\hat k \cdot \vec r - \omega t ) }$ Which if we define the axis these 2 waves to be traveling on as the x-axis, we get $\hat k = \hat x$ for the wave traveling in the positive x, and $\hat k = - \hat x$ for the wave traveling in the negative x direction. Resulting in the 2 waves $Ae^{ i(|\vec k| \cdot x - \omega t} )$ and $Ae^{ i(-|\vec k| \cdot x - \omega t )}$

 

[kuruman]

Resulting in the 2 waves $Ae^{ i(|\vec k| \cdot x - \omega t} )$ and $Ae^{ i(-|\vec k| \cdot x - \omega t )}$

You have answered your own question. When we write $\sin(kx-\omega t)$ the "$k$" in the expression is a magnitude as in $k=\dfrac{2\pi}{\lambda}$ and so is $x$. You should view $kx$ as the result of having taken the dot product. For aesthetic reasons we arrange the phase so that $kx$ appears always positive in the argument of the sinusoid.

Examples
1. Wave traveling in the + x direction, i.e. $\vec k \cdot \vec x=kx$
(a) $\sin(\vec k \cdot \vec x-\omega t)=\sin(kx-\omega t)$
(b) $\cos(\vec k \cdot \vec x-\omega t)=\cos(kx-\omega t)$

2. Wave traveling in the - x direction, i.e. $\vec k \cdot \vec x=-kx$
(a) $\sin(\vec k \cdot \vec x-\omega t)=\sin(-kx-\omega t)=-\sin(kx+\omega t)$
(b) $\cos(\vec k \cdot \vec x-\omega t)=\cos(-kx-\omega t)=\cos(kx+\omega t)$

Do you see the pattern and how the phase determines the direction of propagation?

 

[vanhees71]

It's a question of the relative sign, between the time and space part of the argument, and unfortunately there are different conventions in the literature. The majority of physics textbooks or papers uses the convention
$$f(t,\vec{x})=A \exp(-\mathrm{i} \omega t + \mathrm{i} \vec{k} \cdot \vec{x}).$$
You get the meaning of the direction of $\vec{k}$ by considering planes of constant phase, i.e.,
$$\vec{k} \cdot \vec{x}-\omega t=\text{const}.$$
This tells you that the wave travels in direction of $\vec{k}$.

Another issue are the Green's functions of the Helmholtz operator. These depend also on the convention. In the physicists' convention you get the Helmholtz equation when considering time-harmonic solutions of the wave equation
$$\Box f(t,\vec{x})=J(t,\vec{x}), \quad \Box=\frac{1}{c^2} \partial_t^2 - \Delta,$$
i.e., solutions fulfilling the ansatz
$$f(t,\vec{x})=f_0(\vec{x}) \exp(-\mathrm{i} \omega t),$$
for a source that's also time-harmonic,
$$J(t,\vec{x})=J_0(\vec{x}) \exp(-\mathrm{i} \omega t),$$
where the sign in the exponential is the said convention. Then you get the Helmholtz equation
$$-(\Delta+k^2) f_0(\vec{x})=J_0(\vec{x}), \quad k=\omega/c.$$
The corresponding Green's functions, fulfilling
$$-(\Delta+k^2) G(\vec{x})=\delta(\vec{x}),$$
are not unique but there are two distinct solutions, corresponding to incoming or outgoing spherical waves, i.e.,
$$G_{\pm}(\vec{x})=\frac{\exp(\pm \mathrm{i} k r)}{4 \pi r}, \quad r=|\vec{x}|.$$
The solution with the upper sign are outgoing, with the lower sign incoming waves due to the chosen sign convention for the time-dependence. Usually you need the outgoing wave solution, which in the time domain corresponds to the retarded potential.