Is it possible to evaluate a sum in SymPy without breaking the expression?

[Gaussian97]

TL;DR Summary

SymPy doesn't evaluate a sum

I want to evaluate the sum

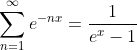
using Python and SymPy, I'm relatively new using SymPy and the first thing I tried was

from sympy import exp, oo, summation, symbols

n, x = symbols('n,x')
summation(exp(-n*x), (n, 1, oo))

But it doesn't work, it just returns the unevaluated sum. I can make it work using

from sympy import exp, oo, summation, symbols

n, x = symbols('n,x')
f = exp(-x)
summation(x**(-n), (n, 1, oo)).subs(x,f)

But I would like to know if it is possible to make it work without need to break the expression into x^n and then substitute x by e^-x.

Thank you

 

[pasmith]

Probably not.

Sympy knows that $\sum_{n=1}^\infty z^n = z/(1 - z)$ when $|z| < 1$, but can't work out that $\sum_{n=1}^\infty e^{-nx}$ reduces to that on substituting $z = e^{-x}$. You have to do that yourself.

You may also want to check the range of your summation:

>>> from sympy import *
>>> x = Dummy('x', real = True, positive=True)
>>> summation(x**n, (n, 1, oo))
Piecewise((_x/(1 - _x), _x < 1), (Sum(_x**n, (n, 1, oo)), True))
>>> summation(x**n, (n, 0, oo))
Piecewise((1/(1 - _x), _x < 1), (Sum(_x**n, (n, 0, oo)), True))