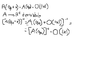- #1
stefano77
- 19
- 8
- TL;DR Summary
- linearization lagrange equation
l am italian student from Milan university, so sorry for my bad english.
l am studying lagrange meccanics. We are linearizating lagrange equations. Here l don't understand how you can expand A matrix, how the function f is derivable, how the inverse matrix A is expanded? l am expanding with q0 center, x is the small displacement . G is a quadratic form.
O(|x|) is order of magnitude
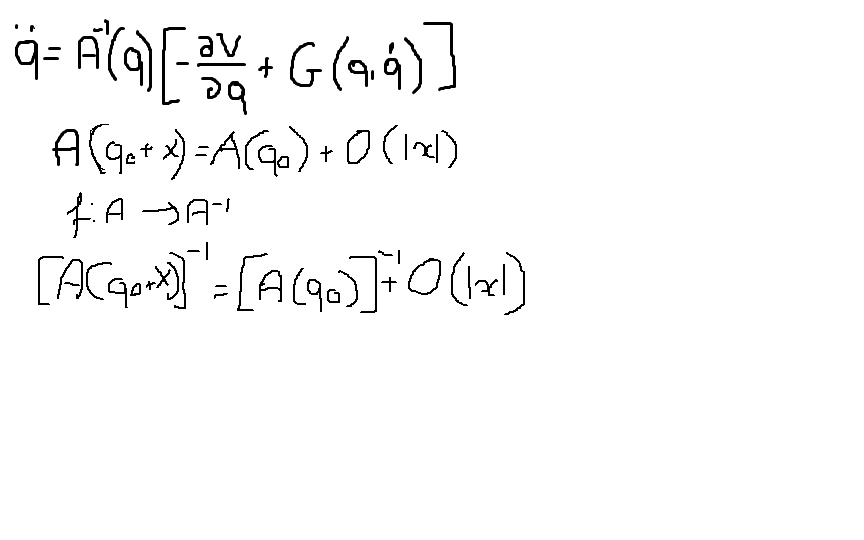
l am studying lagrange meccanics. We are linearizating lagrange equations. Here l don't understand how you can expand A matrix, how the function f is derivable, how the inverse matrix A is expanded? l am expanding with q0 center, x is the small displacement . G is a quadratic form.
O(|x|) is order of magnitude