Lorentz transformation for 3 frames (2 dimensions)

[chaksome]

TL;DR Summary

A discussion about special relativity.

I want to know why an else solution can not get the right answer. And want to know the way to correct this solution.Supposed that a frame S'' is moving in the lab frame at $\beta_x$ in the x-direction, $\beta_y$ in the y-direction, now I want to find out the Lorentz transformation between these frames.

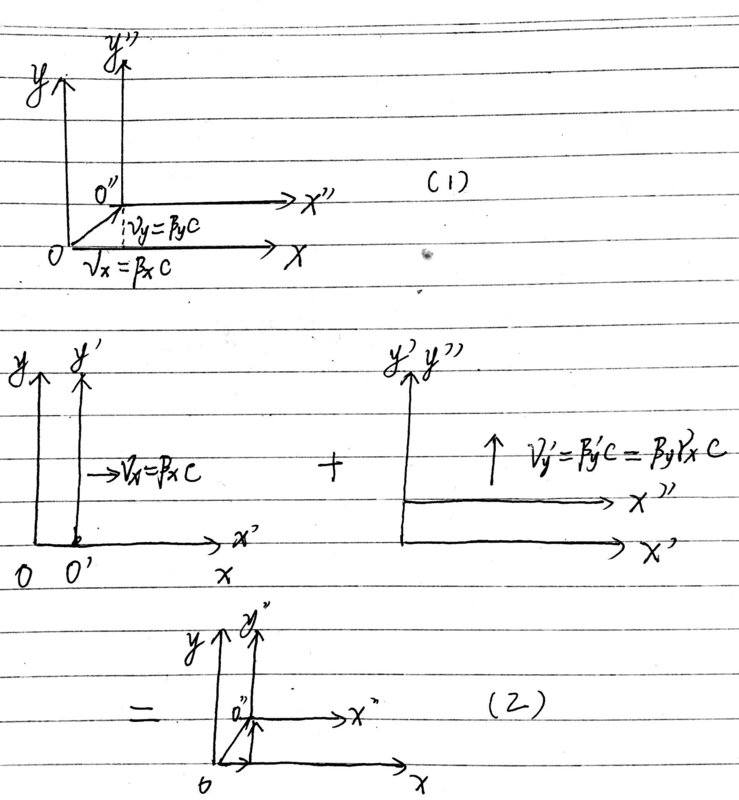
Applying the vector transformation in special relative, I've already worked out the solution like this(and I think it is the correct answer):$$\begin{cases}x''=\frac{\gamma \beta_x^2+\beta_y^2}{\beta_x^2+\beta_y^2}x+\frac{(\gamma-1)\beta_x\beta_y}{\beta_x^2+\beta_y^2}y-\gamma\beta_x ct\\y''=\frac{\gamma \beta_y^2+\beta_x^2}{\beta_x^2+\beta_y^2}y+\frac{(\gamma-1)\beta_x\beta_y}{\beta_x^2+\beta_y^2}x-\gamma\beta_y ct，(1)\\ct''=\gamma ct-\gamma \beta_x x-\gamma\beta_y y\end{cases}$$(and$\gamma=\frac{1}{\sqrt{1-(\beta_x^2+\beta_y^2)}}$)(if there is anything wrong, please point it out)Now I want to solve this problem in a different way (which is valid if the 3 frames are moving in one direction, but fail to work out the right answer in this scene)First, I make a Lorentz transformation between S and S'(which is moving in the frame S at$\beta_x$in the x-direction),and I get the equation$$\begin{cases}x'=\gamma_x(x-\beta_x ct)\\y'=y\\ct'=\gamma_x(ct-\beta_xx)\end{cases}$$Then,I make a Lorentz transformation between S' and S''(according to the velocity-addition formula,S'' is moving in S' at $\beta_y'=\gamma_x\beta_y$in the y-direction),and I get the equation$$\begin{cases}x''=x'\\y''=\gamma_y'(y'-\beta_y' ct')\\t''=\gamma_y'(ct'-\beta_y'y')\end{cases}$$OK,now we solve these equation, and find that$$\begin{cases}x''=\gamma_xx+0y-\gamma_x\beta_xct\\y''=\frac{\gamma}{\gamma_x}y+\gamma\beta_x\beta_yx-\gamma\gamma_x\beta_yct, (2)\\ct''=\gamma ct-\gamma\beta_x x-\gamma\beta_y y\end{cases}$$We can see that (1) is obviously different from (2)I hope to find out the essential cause of this phenomenon(maybe it will refer to the general relativity):What causes the discrepancy between (1) and (2)?Why the ct'' stay consistence?Thanks a million!

 

[mitochan]

Hi.
I would like to give a verification to your (1).

Rotation in xy plane and x-Lorentz transformation are expressed as matrices,
$$R \equiv \begin{pmatrix} cos\phi & sin\phi & 0 \\ -sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ L \equiv \begin{pmatrix} cosh\theta & 0 & sinh\theta \\ 0 & 1 & 0 \\ sinh\theta & 0 & cosh\theta \\ \end{pmatrix}$$
where cosh $\theta$ = $\gamma$, sinh $\theta$ = - $\gamma$v/c.

The successive actions,
1. Rotate the axes so that the S" moves along x axis
2. Do Lorentz transformation for x-moving system
3. Rotate back to original axes
are presented as products of matrices
$$R^{-1}LR= \begin{pmatrix} cosh\theta cos^2\phi +sin^2\phi & (cosh\theta -1)cos\phi sin\phi & sinh\theta cos\phi \\ (cosh\theta -1)cos\phi sin\phi & cosh\theta sin^2\phi + cos^2\phi & sinh\theta sin\phi \\ sinh\theta cos\phi & sinh\theta sin\phi & cosh\theta \\ \end{pmatrix}$$
where matrices product is calculated with above R, L and
$$R^{-1}= \begin{pmatrix} cos\phi & -sin\phi & 0 \\ sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix} \\$$
This meets your (1).

 

[Ibix]

If I'm following correctly what you are doing, the phenomenon is called Wigner rotation, or Thomas rotation. Or Wigner-Thomas rotation. Mathematically, it's a consequence of Lorentz transforms not commuting in general (if the velocities are colinear, they do). Physically, it follows from the fact that something moving along the $y'$ axis has $x'=0$, implying that $x=x(t)$. So "moving along the $y$-axis" and "moving along the $y'$-axis" are two different things - the former implies constant $x$, the latter implies constant $x'$. So compositing movement along $x$ with movement along $y'$ is different from compositing movement along $y$ with movement along $x'$.

 

[chaksome]

Hi.
I would like to give a verification to your (1).

Rotation in xy plane and x-Lorentz transformation are expressed as matrices,
$$R \equiv \begin{pmatrix} cos\phi & sin\phi & 0 \\ -sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ L \equiv \begin{pmatrix} cosh\theta & 0 & sinh\theta \\ 0 & 1 & 0 \\ sinh\theta & 0 & cosh\theta \\ \end{pmatrix}$$
where cosh $\theta$ = $\gamma$, sinh $\theta$ = - $\gamma$v/c.

The successive actions,
1. Rotate the axes so that the S" moves along x axis
2. Do Lorentz transformation for x-moving system
3. Rotate back to original axes
are presented as products of matrices
$$R^{-1}LR= \begin{pmatrix} cosh\theta cos^2\phi +sin^2\phi & (cosh\theta -1)cos\phi sin\phi & sinh\theta cos\phi \\ (cosh\theta -1)cos\phi sin\phi & cosh\theta sin^2\phi + cos^2\phi & sinh\theta sin\phi \\ sinh\theta cos\phi & sinh\theta sin\phi & cosh\theta \\ \end{pmatrix}$$
where matrices product is calculated with above R, L and
$$R^{-1}= \begin{pmatrix} cos\phi & -sin\phi & 0 \\ sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix} \\$$
This meets your (1).

Thanks a lot! It’s absolutely a nice way to get the correct answer. And you have inspired me to some extent that maybe the divergence between (1) and (2) is due to the the effect of the rotation. Do you agree?
And can you please make some analysis about the second solution?
Thanks in advance.
(For the doubt you bring forward in your second message, I think it is actually no relative velocity in the x-direction because:$$v_x'=\frac{v_x-v_x}{1-\frac{v_x^2}{c^2}}=0$$)

 

[chaksome]

If I'm following correctly what you are doing, the phenomenon is called Wigner rotation, or Thomas rotation. Or Wigner-Thomas rotation. Mathematically, it's a consequence of Lorentz transforms not commuting in general (if the velocities are colinear, they do). Physically, it follows from the fact that something moving along the $y'$ axis has $x'=0$, implying that $x=x(t)$. So "moving along the $y$-axis" and "moving along the $y'$-axis" are two different things - the former implies constant $x$, the latter implies constant $x'$. So compositing movement along $x$ with movement along $y'$ is different from compositing movement along $y$ with movement along $x'$.

Though I don't understand the 'Wigner/Tomas/Wigner-Tomas rotation' completely now, but I think you show me a clear road to go by myself. I am so grateful to you for answering my question.

 

[PeroK]

Thanks a lot! It’s absolutely a nice way to get the correct answer. And you have inspired me to some extent that maybe the divergence between (1) and (2) is due to the the effect of the rotation. Do you agree?
And can you please make some analysis about the second solution?
Thanks in advance.
(For the doubt you bring forward in your second message, I think it is actually no relative velocity in the x-direction because:$$v_x'=\frac{v_x-v_x}{1-\frac{v_x^2}{c^2}}=0$$)

If you look at the solution from @mitochan, it doesn't actually say explicitly how the axes in S'' are defined. And, in fact, in order to do the inverse rotation $R^{-1}$ you must orient the axes in S'' so that the motion of S (in S'') is at the same angle as the motion of S'' in S. In this case $\phi$. (Although, of course, in the opposite direction.)

With this definition for the axes in S'' you get the "correct" transformation.

If you take your second approach and you map the y'' axis: i.e. the points that have x-y coordinates $(0, y'')$ at some fixed time $t''$, you will see that this does not map to a vertical line in S. (This is the basis of the Wigner rotation.)

You've effectively done a valid two-stage transformation: but you have transformed to a coordinate system in S'' which is different from the one you got by the first method.

You could work out the angle at which S in moving in S'' in this case. Then, if you really wanted to, you could add a final rotation to rotate the axes in S'' so that S is moving at angle $\phi$ and this should bring you back to the first solution.

 

[chaksome]

If you look at the solution from @mitochan, it doesn't actually say explicitly how the axes in S'' are defined. And, in fact, in order to do the inverse rotation $R^{-1}$ you must orient the axes in S'' so that the motion of S (in S'') is at the same angle as the motion of S'' in S. In this case $\phi$. (Although, of course, in the opposite direction.)

With this definition for the axes in S'' you get the "correct" transformation.

If you take your second approach and you map the y'' axis: i.e. the points that have x-y coordinates $(0, y'')$ at some fixed time $t''$, you will see that this does not map to a vertical line in S. (This is the basis of the Wigner rotation.)

You've effectively done a valid two-stage transformation: but you have transformed to a coordinate system in S'' which is different from the one you got by the first method.

You could work out the angle at which S in moving in S'' in this case. Then, if you really wanted to, you could add a final rotation to rotate the axes in S'' so that S is moving at angle $\phi$ and this should bring you back to the first solution.

I gradually come to understand, the what you say also explain the phenomenon that expression of ct” in (1)and(2) are the same.
Thanks a lot!

 

[chaksome]

WOW! I worked out the matrix of the rotation$$R=\begin{pmatrix}cos\varepsilon&sin\varepsilon&0\\-sin\varepsilon&cos\varepsilon&0\\0&0&1\end{pmatrix}$$
and$$sin\varepsilon=\frac{\gamma-1}{\gamma}\frac{\beta_x\beta_y\gamma_x}{\beta_x^2+\beta_y^2}$$
And I've read some paper about the Thomas precession, and I find it more and more interesting to learn more things in this field.
Thank you all again~

 

[mitochan]

As for your (2) I write down corresponding matrices.
$$L_1\equiv \begin{pmatrix} c_1 & 0 & s_1 \\ 0 & 1 & 0 \\ s_1 & 0 & c_1 \\ \end{pmatrix}$$

$$L_2\equiv \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_2 & s_2 \\ 0 & s_2 & c_2 \\ \end{pmatrix}$$
where $c_i\equiv cosh\theta_i$, $s_i \equiv sinh\theta_i,i=1,2$
index i=1 correspond to x-axis Lorentz transformation and i=2 corresponds to that of y axis.

Matrices for successive Lorentz transformations are
$$L_2 L_1 = \begin{pmatrix} c_1 & 0 & s_1 \\ s_1s_2 & c_2 & s_2c_1 \\ s_1c_2 & s_2 & c_1c_2 \\ \end{pmatrix}$$ and $$L_1 L_2 = \begin{pmatrix} c_1 & s_1s_2 & s_1c_2 \\ 0 & c_2 & s_2 \\ s_1 & c_1s_2 & c_1c_2 \\ \end{pmatrix}$$
We see ,if my calculation right, $$L_2 L_1 = (L_1 L_2)^{T}$$

 

[mitochan]

(contd.)
$$L_1L_2-L_2L_1= \begin{pmatrix} 0 & s_1s_2 & s_1(c_2-1) \\ -s_1s_2 & 0 & s_2(1-c_1) \\ s_1(1-c_2) & s_2(c_1-1) & 0 \\ \end{pmatrix}$$
Say $\theta_i<<1$ leaving only order 2 and neglecting highers, approximately,
$$L_1L_2-L_2L_1= \begin{pmatrix} 0 & \theta_1\theta_2 & 0 \\ -\theta_1\theta_2 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}$$
Only rotation components survive. So application order of infinitely small Lorentz transformation, i.e. x first then y or y first then x, results difference of rotation.

 

[chaksome]

As for your (2) I write down corresponding matrices.
$$L_1\equiv \begin{pmatrix} c_1 & 0 & s_1 \\ 0 & 1 & 0 \\ s_1 & 0 & c_1 \\ \end{pmatrix}$$

$$L_2\equiv \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_2 & s_2 \\ 0 & s_2 & c_2 \\ \end{pmatrix}$$
where $c_i\equiv cosh\theta_i$, $s_i \equiv sinh\theta_i,i=1,2$
index i=1 correspond to x-axis Lorentz transformation and i=2 corresponds to that of y axis.

Matrices for successive Lorentz transformations are
$$L_2 L_1 = \begin{pmatrix} c_1 & 0 & s_1 \\ s_1s_2 & c_2 & s_2c_1 \\ s_1c_2 & s_2 & c_1c_2 \\ \end{pmatrix}$$ and $$L_1 L_2 = \begin{pmatrix} c_1 & s_1s_2 & s_1c_2 \\ 0 & c_2 & s_2 \\ s_1 & c_1s_2 & c_1c_2 \\ \end{pmatrix}$$
We see ,if my calculation right, $$L_2 L_1 = (L_1 L_2)^{T}$$

wah！So many interesting things can be found through your calculation.Yesterday, I was thinking about the physical meaning of the equation,$$L_1L_2=(L_2L_1)^T$$
But I failed to find a clear meaning in physics.
Is that mean a kind of symmetry?
And~according to your theory, the transformation of time is also different if we change the application order of the Lorentz Transformation when the $\theta _i$ is larger.How do we think about it?

 

[mitochan]

Hi.
How about challenging finding the components of the following L and R?

$$L_2L_1=LR$$
where R is mentioned in my post #2 and L is a symmetric matrix representing Lorentz transformation, or boost.

If you succeed, you can learn that two successive boosts are interpreted as successive rotation and a boost.

 

[chaksome]

Hi.
How about challenging finding the components of the following L and R?

$$L_2L_1=LR$$
where R is mentioned in my post #2 and L is a symmetric matrix representing Lorentz transformation, or boost.

If you succeed, you can learn that two successive boosts are interpreted as successive rotation and a boost.

Hello,thank you for your patience and the guidance~
Do you mean that:
$$R^{-1}LR=(LR^{-1})^TR=L^TR^2$$
Then we can define that
$$R^*\equiv R, L^*\equiv L^T=L$$
and we can interpret the successive boosts as$L^*R^*R^*$,or $LRR$
$$R^*=\begin{pmatrix}cos\epsilon&sin\epsilon&0\\-sin\epsilon&cos\epsilon&0\\0&0&1\end{pmatrix}$$
$$L^*=\begin{pmatrix}cosh\theta&0&sinh\theta\\0&1&0\\sinh\theta&0&cosh\theta\end{pmatrix}$$
$$LRR=
\begin{pmatrix}
cosh\theta cos^2\phi +sin^2\phi & (cosh\theta -1)cos\phi sin\phi & sinh\theta cos\phi \\
(cosh\theta -1)cos\phi sin\phi & cosh\theta sin^2\phi + cos^2\phi & sinh\theta sin\phi \\
sinh\theta cos\phi & sinh\theta sin\phi & cosh\theta \\
\end{pmatrix}$$
which meets my (1)

 

[mitochan]

(correction and supplement to my post #12)
Hypothesis : First x- then y- boosts is interpreted as first boost in one direction then rotation, i.e.
$$L_2 L_1 =RL$$
If so
$$R^{-1} L_2 L_1 =L$$
with $R^{-1}$ in post #2, $L_2L_1$ in post #9 and careful choice of angle $\phi$, RHS L would become a symmetric matrix representing boost.

My preliminary calculation suggests such a coordinated rotation angle be
$$tan\phi=\frac{s_1 s_2 }{c_1+c_2}$$
and then L becomes boost matrix for boost velocity $$(c\beta_x,\ c\gamma_x\beta_y)$$, which is a kind you introduced in post #1, but not successive boosts but a single boost.
Further, formula
$$R=L_2L_1L^{-1}$$
suggests that a rotation is interpreted and represented as three successive boosts of first $(-c\beta_x,-\ c\gamma_x\beta_y)$, then $c\beta_x$ and at last $c\beta_y$.

I should appreciate it if you check calculations and hopefully verify it.

 

[chaksome]

$$tan\phi=\frac{s_1 s_2 }{c_1+c_2}$$

I finally found it exactly meet what I work out in my #8, and I try to follow your thoughts and verify that the angle you show is right. Thank you for giving me another opinion of this question ~

 

[mitochan]

(correction of sign in #14 and supplements)

$$sin\phi=-\frac{s_1s_2}{c_1c_2+1}$$
$$cos\phi=\frac{c_1+c_2}{c_1c_2+1}$$
$$tan\phi=-\frac{s_1s_2}{c_1+c_2}$$

$$L=\begin{pmatrix} 1+\frac{s_1^2c_2^2}{c_1c_2+1} & \frac{s_1s_2c_2}{c_1c_2+1} & s_1c_2 \\ \frac{s_1s_2c_2}{c_1c_2+1} & 1+\frac{s_2^2}{c_1c_2+1} & s_2 \\ s_1c_2 & s_2 & c_1c_2 \\ \end{pmatrix}$$

 

[mitochan]

(continued)

Indtroducing $s'_2=s_2/c_1$,

$$L=\begin{pmatrix} 1+\frac{s_1^2 c_2^2}{c_1c_2+1} & \frac{s_1s_2' c_1c_2}{c_1c_2+1} & s_1c_2 \\ \frac{s_1s_2'c_1c_2}{c_1c_2+1} & 1+\frac{s_2'^2c_1^2}{c_1c_2+1} & s_2'c_1 \\ s_1c_2 & s_2'c_1 & c_1c_2 \\ \end{pmatrix}$$

Symmetry between 1 and 2 is apparent.

$$L=\begin{pmatrix} 1+\alpha (v_1/c)^2 & \alpha (v_1/c)(v'_2/c) & -(v_1/c)c_1c_2 \\ \alpha (v_1/c)(v'_2/c) & 1+\alpha (v'_2/c)^2 & -(v'_2/c)c_1c_2 \\ -(v_1/c)c_1c_2 & -(v'_2/c)c_1c_2 & c_1c_2 \\ \end{pmatrix}$$
where
$$\alpha=\frac{c_1^2c_2^2}{c_1c_2+1}$$
$$c_i=\frac{1}{\sqrt{1-v_i^2/c^2}}=\gamma_i$$
$$v_i/c=-tanh\theta_i=-s_i/c_i$$
$$v'_2=v_2/c_1$$

This matrix is expected to represent boost for velocity $(v_1,v_2/\gamma_1)$.
Factor $1/\gamma_1$ reduces velocity of the second boost in original S-S'-S" procedure. This is interpreted to take place by time dilation of S' ,where $v_2$ is measured, against S.

In this synthesized boost $s_2$ is reduced to $s'_2=s_2/\gamma_1$. however $c_2$ appears with no modification in the boost matrix. I would like to understand it in depth.

 

[mitochan]

(correction)
$$-v_i/c=tahn\theta_i=s_i$$

Following the prescription in post #2, i.e. rotate, x-boost and rotate back, I calculated matrices to be

$$L=R^{-1}(\phi)L_1(V)R(\phi)$$

where

$$V^2/c^2\equiv v_1^2/c^2 + \frac{v_2^2/c^2}{\gamma_1^2}=v_2^2+ \frac {v_1^2/c^2} {\gamma_2^2}$$
,symmetric between 1 and 2, and
$$=1-\frac{1}{\gamma_1^2\gamma_2^2}\equiv 1-\frac{1}{\gamma^2}$$
$$\phi=tan^{-1}\frac{v_2}{v_1\gamma_1}$$
Going backto post #14 with this,

$$L_2(v_2)L_1(v_1)=R(\Phi)R^{-1}(\phi)L_1(V)R(\phi)$$

where

$$\Phi=-tan^{-1}\frac{v_1v_2/c^2}{\gamma_1\gamma_2(\gamma_1+\gamma_2)}$$

I have not calculated on the commutation but hopefully expect

$$L_1(v_1)L_2(v_2)=R(\Phi)R^{-1}(\phi)L_1(V)R(\phi)$$

but where $\phi$ has different value from the above case, so

$$\phi=tan^{-1}\frac{v_2\gamma_2}{v_1}$$

with reminding that suffix 1 denotes x coordinate and 2 denotes y coordinate.

So I summerize here my understanding of making $L_1L_2$ and $L_1L_2$ transformations in S,
- First, boost with velocities of the same magnitude but different directions,
- Then rotate with the same angle.

 

[mitochan]

And~according to your theory, the transformation of time is also different if we change the application order of the Lorentz Transformation when the $\theta _i$ is larger.How do we think about it?

From the previous post the both undertake the rotation of the same angle so common rotation component coefficicent $v_1v_2/c^2$ as the top order. Difference in boost directions effects in higher orders.

Say "boosts go-around",

$$L_2(-v_2)L_1(-v_1)L_2(v_2)L_1(v_1)$$
$$=R(\Phi)R^{-1}(\phi+\pi/2)L_1(V)R(\phi+\pi/2)R(\Phi)R^{-1}(\phi)L_1(V)R(\phi) \approx R(2\Phi)$$

for infinitesimal boosts. Rotation would be interpreted as integrated infinitesimal boost go around sets.

Obviously,

$$L_1(-v_1)L_2(-v_2)L_2(v_2)L_1(v_1)=I$$

 

[mitochan]

(correction) angle for inverse direction is $\phi+\pi$, not $\phi+\pi/2$.