Mahesh's question via email about a Runge-Kutta scheme

[Prove It]

View attachment 9657

To apply this Runge-Kutta scheme, we will need to write our second order DE as a system of first order DEs.

Let $\displaystyle u = y $ and $\displaystyle v = y' $, then we have

$\displaystyle \begin{align*} y'' + 4\,v - 7\,u^2 &= 0.2 \\
y'' &= 0.2 - 4\,v + 7\,u^2 \end{align*} $

So our system of first order DEs is:

$\displaystyle \begin{align*} u' &= v , \quad \quad \quad \quad \quad \quad \quad \, u\left( 0 \right) = 3 \\
v' &= 0.2 - 4\,v + 7\,u^2 , \quad v\left( 0 \right) = 0 \end{align*} $

Now we can apply the Runge-Kutta scheme. Note that $\displaystyle f\left( u,v \right) = v $ and $\displaystyle g\left( u,v \right) = 0.2 - 4\,v + 7\,u^2 $, and the step size is $\displaystyle h = 0.05 $.

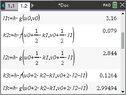
I have used my CAS to solve this.

View attachment 9659

View attachment 9660

View attachment 9661

View attachment 9662

View attachment 9663

Moving along two steps of size $\displaystyle h = 0.05 $ gets us to $\displaystyle t = 0.1 $, and since $\displaystyle u = y $, that means we have $\displaystyle y\left( 0.2 \right) = u_2 = 3.28623 $.

 

[jvicens]

Hello,

Thank you for sharing your approach to solving this problem using the Runge-Kutta scheme. It's great to see how you were able to break down the second order DE into a system of first order DEs and then apply the scheme to solve for $\displaystyle y\left( 0.2 \right) $.

One thing I would like to add is that the Runge-Kutta scheme is a numerical method for solving differential equations, so it is not necessary to use a CAS to obtain the solution. However, using a CAS can be helpful for checking your work and verifying the accuracy of the solution.

Overall, your explanation was clear and easy to follow. Keep up the good work!