- #1
roam
- 1,271
- 12
- Homework Statement
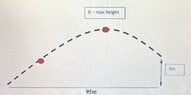
- A ball has travelled a horizontal distance of 95m and landed 9m up in a stand as shown in the diagram attached below. The time of the flight was 4.5s. Calculate the angle at which the ball was hit.
- Relevant Equations
- ##\theta=\arctan(\frac{v_{y}}{v_{x}})##
##v^2_y = v^2_{0y} - 2 g(y-y_0)##
##v## indicates velocity and ##y## is height.
I am trying to find the launch angle ##\theta## using the relationship:
##\theta=\arctan(\frac{v_{y}}{v_{x}})##
So, ignoring attenuation due to air resistance, we have a constant horizontal velocity:
##v_x = d_x/t = 95m/4.5s \approx 21 m/s##
But what value do we use for ##v_y## which is not constant? It has a positive value until the ball reaches the apex of the trajectory where ##v_y=0##. Or is there a simpler way to approach this problem?
Any help is greatly appreciated.
##\theta=\arctan(\frac{v_{y}}{v_{x}})##
So, ignoring attenuation due to air resistance, we have a constant horizontal velocity:
##v_x = d_x/t = 95m/4.5s \approx 21 m/s##
But what value do we use for ##v_y## which is not constant? It has a positive value until the ball reaches the apex of the trajectory where ##v_y=0##. Or is there a simpler way to approach this problem?
Any help is greatly appreciated.