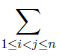- #1
NicolaiTheDane
- 100
- 10
Homework Statement
Through out my linear algebra book, this weird summation sign has started appearing, and I haven't been able to find anything on it online. Can someone please explain how I'm suppose to read this:
Homework Equations
The Attempt at a Solution
Now in the first case, I could at least work with it, as I could read that notion "i in I" means a family of vectors/scalars, where "I" denotes the entire family, and i denotes an individual vector/scalar. So basically what this means is:
v1*a1+v2*a2+..+vi*ai (where i denotes the last elements)
Now the problem is that the second one, I cannot just read an example and "just do it" as that one from an actually assignment. I need to understand what it actually means. My teacher has barely any time to explain things, as he has his own stuff to get through, but basically from what I can gather, it a sum within a sum. However exactly how this is suppose to work, from the given notation, I haven't got the faintest idea.
Thanks in advance for any all assistance.