Orthogonality of Wannier functions

[Sheng]

I have trouble reconciling orthogonality condition for Wannier functions using both continuous and discrete k-space. I am using the definition of Wannier function and Bloch function as provided by Wikipedia (https://en.wikipedia.org/wiki/Wannier_function).

Wannier function:

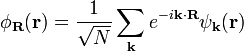Bloch function:

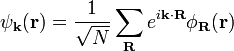
I can understand the orthogonality condition for Wannier functions in the discrete k-space as provided in Wikipedia:

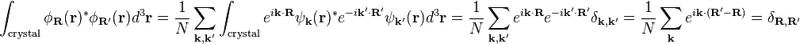But when I transform the summation over k-point to the integral representation using the relation:
$$ \sum_{\mathbf{k}} \rightarrow \frac{N\Omega}{(2\pi)^3} \int_{BZ} d\mathbf{k} $$
where N is the number of unit cell and $\Omega$ is the primitive cell volume, so that
$$ \phi_{n\mathbf{R}}(\mathbf{r}) = \frac{\sqrt{N}\Omega}{(2\pi)^3} \int_{BZ} e^{-i\mathbf{k \cdot R}} \psi_{n\mathbf{k}}(\mathbf{r}) d\mathbf{k} $$
which I cannot regain the orthogonality behaviour.

These are my calculations:
$$
\langle \phi_{n\mathbf{R}}(\mathbf{r}) \vert \phi_{m\mathbf{R'}}(\mathbf{r}) \rangle = N \left( \frac{\Omega}{(2\pi)^3} \right) ^2 \int_V \int_{BZ} \int_{BZ} e^{i\mathbf{k \cdot R}} e^{-i\mathbf{k' \cdot R'}} \psi^*_{n\mathbf{k}}(\mathbf{r}) \psi_{m\mathbf{k'}}(\mathbf{r}) d\mathbf{k'} d\mathbf{k} d\mathbf{r}
$$
where V is the total volume included in the Born von Karman periodic boundary condition. Using
$$
\int_V \psi^*_{n\mathbf{k}}(\mathbf{r}) \psi_{m\mathbf{k'}}(\mathbf{r}) d\mathbf{r} = \delta_{mn}\delta(\mathbf{k-k'})
$$
I get
$$
\langle \phi_{n\mathbf{R}}(\mathbf{r}) \vert \phi_{m\mathbf{R'}}(\mathbf{r}) \rangle = N \left( \frac{\Omega}{(2\pi)^3} \right) ^2 \int_{BZ} \int_{BZ} e^{i\mathbf{k \cdot R}} e^{-i\mathbf{k' \cdot R'}} \delta_{mn} \delta(\mathbf{k-k'}) d\mathbf{k'} d\mathbf{k}
$$
Using (I don't know this one is correct or not)
$$
\int_{BZ} e^{-i\mathbf{k' \cdot R'}} \delta(\mathbf{k-k'}) d\mathbf{k'} = \frac{(2\pi)^3}{\Omega} e^{-i\mathbf{k \cdot R'}}
$$
then
$$
\langle \phi_{n\mathbf{R}}(\mathbf{r}) \vert \phi_{m\mathbf{R'}}(\mathbf{r}) \rangle = \delta_{mn} N \frac{\Omega}{(2\pi)^3} \int_{BZ} e^{i\mathbf{k \cdot (R-R')}} d\mathbf{k}
$$
With
$$
\frac{\Omega}{(2\pi)^3} \int_{BZ} e^{i\mathbf{k \cdot (R-R')}} d\mathbf{k} = \delta_{\mathbf{R,R'}}
$$
Finally I get
$$
\langle \phi_{n\mathbf{R}}(\mathbf{r}) \vert \phi_{m\mathbf{R'}}(\mathbf{r}) \rangle = N \delta_{mn} \delta_{\mathbf{R,R'}}
$$
which contains an additional term N.

Anyone can point out my mistake?

 

[DrDu]

$$
\int_{BZ} e^{-i\mathbf{k' \cdot R'}} \delta(\mathbf{k-k'}) d\mathbf{k'} = e^{-i\mathbf{k \cdot R'}}
$$

 

[Sheng]

Thanks for your reply. I am tempted to use that one because it is closer to the solution I want. But even then the final form is just
$$
\langle \phi_{n\mathbf{R}}(\mathbf{r}) \vert \phi_{m\mathbf{R'}}(\mathbf{r}) \rangle = N \frac{\Omega}{(2\pi)^3} \delta_{mn} \delta_{\mathbf{R,R'}}
$$
which differs from the discrete version.

I figure that this question contains more fundamental aspect I might want to be sure of first, before I continue to tackle the previous question.
Thank you.

 

[DrDu]

I
But when I transform the summation over k-point to the integral representation using the relation:
$$ \sum_{\mathbf{k}} \rightarrow \frac{N\Omega}{(2\pi)^3} \int_{BZ} d\mathbf{k} $$

Why only BZ on the RHS?

 

[Sheng]

It is not? It is in accordance with that on Wikipedia

$\Omega$ in this case is the Brillouin zone volume. Most of the references I consult automatically limit the integration region to the first Brillouin zone.

If not then how do I limit the integration region to only the first Brillouin zone? Using the same concept as in real space like introducing $\mathbf{k \rightarrow k+G}$ and $\sum_{\mathbf{G}}$ ?

 

[DrDu]

If $k_i=2\pi n_i/L$ with $V=L^3$ being the crystal volume ($V=N\Omega$), then $\sum_\mathbf{k}=\sum_\mathbf{n}=\frac{V}{(2\pi)^3} \sum_n \frac{(2\pi)^3}{V}=\frac{V}{(2\pi)^3} \int d\mathbf{n} \frac{(2\pi)^3}{V}=\frac{V}{(2\pi)^3} \int d\mathbf{k}$.
If the integrand is periodic, then $\int_V d\mathbf{k}=N\int_{BZ} d\mathbf{k}$.

 

[Sheng]

Ok so now $\sum_{\mathbf{k}} \rightarrow \frac{N^2\Omega}{(2\pi)^3} \int_{BZ} d\mathbf{k}$ and
$$
\phi_{n\mathbf{R}}(\mathbf{r}) = \frac{N^{3/2}\Omega}{(2\pi)^3} \int_{BZ} e^{-i\mathbf{k \cdot R}} \psi_{n\mathbf{k}}(\mathbf{r}) d\mathbf{k}
$$
and the final form become
$$
\langle \phi_{n\mathbf{R}}(\mathbf{r}) \vert \phi_{m\mathbf{R'}}(\mathbf{r}) \rangle = N^3 \frac{\Omega}{(2\pi)^3} \delta_{mn} \delta_{\mathbf{R,R'}}
$$
which I feel weird.

 

[DrDu]

$$
\frac{N\Omega}{(2\pi)^3} \int_{BZ} e^{i\mathbf{k \cdot (R-R')}} d\mathbf{k} = \delta_{\mathbf{R,R'}}
$$

 

[DrDu]

Using
$$
\int_V \psi^*_{n\mathbf{k}}(\mathbf{r}) \psi_{m\mathbf{k'}}(\mathbf{r}) d\mathbf{r} = \delta_{mn}\delta(\mathbf{k-k'})
$$

That's also not correct, you have
$$
\int_V \psi^*_{n\mathbf{k}}(\mathbf{r}) \psi_{m\mathbf{k'}}(\mathbf{r}) d\mathbf{r} = \delta_{mn}\delta_{kk'}
$$
and you can't simply replace Kronecker by Dirac.

 

[Sheng]

Since $\sum_\mathbf{k}=\sum_\mathbf{n}=\frac{V}{(2\pi)^3} \sum_n \frac{(2\pi)^3}{V}=\frac{V}{(2\pi)^3} \int d\mathbf{n} \frac{(2\pi)^3}{V}=\frac{V}{(2\pi)^3} \int d\mathbf{k}$
we have made a transformation from discrete k to continuous k, then why can't we use dirac delta function?

 

[DrDu]

You can, but there will be an N dependent prefactor

 

[Sheng]

Sorry, I forgot to mention that the summation on k is restricted to first Brillouin zone only, in that case does $\sum_{\mathbf{k} \in BZ} \rightarrow \frac{N\Omega}{(2\pi)^3} \int_{BZ} d\mathbf{k}$
apply? I mean directly restricting the integration region to BZ.

$$
\frac{N\Omega}{(2\pi)^3} \int_{BZ} e^{i\mathbf{k \cdot (R-R')}} d\mathbf{k} = \delta_{\mathbf{R,R'}}
$$

I have some doubts on this.

From Ashcroft and Mermin's Solid State Physics Appendix F, it is given that
$$
\sum_{\mathbf{k} \in BZ} e^{i\mathbf{k \cdot R}} = N \delta_{\mathbf{R},0}
$$
if the above transformation is true then
$$
\frac{\Omega}{(2\pi)^3} \int_{BZ} e^{i\mathbf{k \cdot (R-R')}} d\mathbf{k} = \delta_{\mathbf{R,R'}}
$$
is it?

You can, but there will be an N dependent prefactor

Care to provide some reasoning on this?

 

[DrDu]

Care to provide some reasoning on this?

No, that's your job!
Do not simply take over some equations from books or even worse, Wikipedia. They may use different conventions. Try to count the number of k states in the BZ. Transform the sums to integrals as I have shown you. Use the basic relations for delta functions and Kronecker delta.

 

[DrDu]

Sorry, I forgot to mention that the summation on k is restricted to first Brillouin zone only, in that case does $\sum_{\mathbf{k} \in BZ} \rightarrow \frac{N\Omega}{(2\pi)^3} \int_{BZ} d\mathbf{k}$
apply? I mean directly restricting the integration region to BZ.

Ok, this removes at least two of the dubious N's.

I have some doubts on this.

From Ashcroft and Mermin's Solid State Physics Appendix F, it is given that
$$
\sum_{\mathbf{k} \in BZ} e^{i\mathbf{k \cdot R}} = N \delta_{\mathbf{R},0}
$$
if the above transformation is true then
$$
\frac{\Omega}{(2\pi)^3} \int_{BZ} e^{i\mathbf{k \cdot (R-R')}} d\mathbf{k} = \delta_{\mathbf{R,R'}}
$$
is it?
Care to provide some reasoning on this?

Yes, I think this is correct and maybe I stepped in the same trap as you did. Namely I assumed that $\delta(R-R')=\delta_{R,R'}$.
So I think the problem is that you changed $\delta_{k,k'}$ to $\delta(k-k')$.
But $\sum_k \delta_{k,0}=1$ while $V/(2\pi)^3 \int_{BZ} dk \delta(k)=V/(2\pi)^3$. So you should substitute $\delta_{k,k'}\to (2\pi)^3/V \delta(k-k')$