Oscillation of a solid hemisphere

[Saitama]

Homework Statement

I don't have the exact wordings of the problem statement. I hope the following is enough to understand the problem.

A solid hemisphere is kept on a plane horizontal frictionless surface. The hemisphere is made to tumble (or toss, I am not sure about the correct word). Find the time period of oscillation.

The mass of hemisphere is M and radius is R.

Homework Equations

The Attempt at a Solution

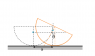
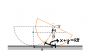
I have described the situation in the attachment.

The CM of hemisphere is at a distance 3R/8 from the centre of base of hemisphere. To find the time period, I am thinking of writing down the expression for energy at any instant and then set its time derivative to zero.

The orange coloured sketch is the new position of hemisphere. For the energy equation, I need the angular velocity, velocity of CM and height of CM from the ground.

For angular velocity, I write $d\theta/dt$. I can also find the height of CM but I have trouble finding the velocity of CM or specifically, the horizontal component of velocity. How do I find the horizontal displacement ($x$) of CM? I have found out rest of the variables in terms of $\theta$ and I am stuck on finding the horizontal displacement from hours. (I hope the sketch is easily decipherable).

Any help is appreciated. Thanks!

 

[haruspex]

"base" might be a bit ambiguous here. I guess you mean 3R/8 from centre of whole sphere.
Can you see straightaway what the displacement of the point of contact is as a function of theta? That gives you the displacement of the centre of the sphere. Then you just need a small correction to come back to x.

 

[consciousness]

See the figure to get x as function of theta.
Since the hemisphere doesn't lose contact with the ground, the distance between the "vertex" of the hemisphere and the point of contact is x i.e. distance traveled.

Edit: Just noticed that your x is distance traveled by CM. To correct for this add the small distance between CM and vertical axis passing through point of contact with ground. My figure is wrong.

Edit 2: Figure now corrected

 

[ehild]

A solid hemisphere is kept on a plane horizontal frictionless surface. The hemisphere is made to tumble (or toss, I am not sure about the correct word). Find the time period of oscillation.

The orange coloured sketch is the new position of hemisphere. For the energy equation, I need the angular velocity, velocity of CM and height of CM from the ground.

For angular velocity, I write $d\theta/dt$. I can also find the height of CM but I have trouble finding the velocity of CM or specifically, the horizontal component of velocity. How do I find the horizontal displacement ($x$) of CM?

Is the CM displaced at all if the surface is frictionless?

ehild

 

[haruspex]

Is the CM displaced at all if the surface is frictionless?

ehild

Well spotted.

 

[Saitama]

Hi ehild, haruspex and consciousness! :)

Is the CM displaced at all if the surface is frictionless?

ehild

Yes, you are right, I am sorry about that.

If I modify the question this way, let the surface provides enough friction to allow pure rolling, would it be correct?

See the figure to get x as function of theta.
Since the hemisphere doesn't lose contact with the ground, the distance between the "vertex" of the hemisphere and the point of contact is x i.e. distance traveled.

Edit: Just noticed that your x is distance traveled by CM. To correct for this add the small distance between CM and vertical axis passing through point of contact with ground. My figure is wrong.

Edit 2: Figure now corrected

Ah yes, thanks consciousness!

So we have $x+y'=R\theta$ (I will use $y$ to denote the vertical displacement of CM) where $y'=(3R/8)\sin\theta$, hence $x=R\theta-(3R/8)\sin\theta$.

The vertical displacement of CM is given by $y=(3R/8)(1-\cos\theta)$. Hence

$$\frac{dx}{dt}=\left(R-\frac{3R}{8}\cos\theta\right)\left(\frac{d\theta}{dt}\right)$$
$$\frac{dy}{dt}=\frac{3R}{8}\sin\theta \left(\frac{d\theta}{dt}\right)$$

The energy at any instant of time,
$$E=\frac{1}{2}M\left(\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt} \right)^2 \right)+\frac{1}{2}I\left(\frac{d\theta}{dt}\right)^2+mgh(\theta)$$

where $I$ is the moment of inertia of hemisphere about CM, I found it to be:
$$I=\frac{83}{320}MR^2$$
and
$$h(\theta)=R-\frac{3R}{8}\cos\theta$$
I plugged in the expressions for dx/dt and dy/dt and got:
$$E=\frac{1}{2}M\left(\frac{73}{64}R^2-\frac{3R^2}{4}\cos\theta\right)\left(\frac{d\theta}{dt}\right)^2+\frac{1}{2}\frac{83MR^2}{320}\left(\frac{d\theta}{dt}\right)^2+Mg\left(R-\frac{3R}{8}\cos\theta\right)$$

This is getting a bit dirty so I would like to know if I am correct so far. :)

 

[consciousness]

I get a different value for moment of inertia.

Moment of inertia of a solid hemisphere about the axis passing through the center of its base let's say I.
$$I=\frac{1}{5}MR^2$$
We want to find I_COM moment of inertia about axis passing the COM of the body parallel to the plane of the base let's say x. By parallel axis theorem,
$$I=x+Mr^2$$
$$x=\frac{1}{5}MR^2-\frac{9}{64}MR^2$$
$$x=\frac{19}{320}MR^2$$
Don't see any error apart from this

 

[haruspex]

Moment of inertia of a solid hemisphere about the axis passing through the center of its base let's say I.
$$I=\frac{1}{5}MR^2$$

2/5. Pranav-Arora's 83/320 is correct.

 

[haruspex]

If I modify the question this way, let the surface provides enough friction to allow pure rolling, would it be correct?

Well, which is the actual question? Both make sense.

 

[haruspex]

I plugged in the expressions for dx/dt and dy/dt and got:
$$E=\frac{1}{2}M\left(\frac{73}{64}R^2-\frac{3R^2}{4}\cos\theta\right)\left(\frac{d\theta}{dt}\right)^2+\frac{1}{2}\frac{83MR^2}{320}\left(\frac{d\theta}{dt}\right)^2+Mg\left(R-\frac{3R}{8}\cos\theta\right)$$

This is getting a bit dirty so I would like to know if I am correct so far. :)

Looks right to me. You can simplify a little by taking the zero potential at height 5R/8 instead of ground. Collecting up the $MR^2\frac{d\theta}{dt}^2$ terms yields a much simpler coefficient.

 

[consciousness]

2/5. Pranav-Arora's 83/320 is correct.

2/5 is for a solid sphere. For a hemisphere divide it by two.

 

[haruspex]

2/5 is for a solid sphere. For a hemisphere divide it by two.

It's half the mass. Formula is still 2Mr²/5.

 

[consciousness]

It's half the mass. Formula is still 2Mr²/5.

You are right I messed up

 

[Saitama]

Collecting up the $MR^2\frac{d\theta}{dt}^2$ terms yields a much simpler coefficient.

Yes, you are right, it gets really simple with that. I got:
$$E=\frac{1}{2}MR^2\left(\frac{7}{5}-\frac{3}{4}\cos\theta\right)\left(\frac{d\theta}{dt}\right)^2+mgR\left(1-\frac{3}{8}\cos\theta\right)$$
Differentiating wrt time,
$$\frac{dE}{dt}=\frac{1}{2}MR^2\left(\frac{3}{4}\sin\theta\dot{\theta}^3+\left(\frac{7}{5}-\frac{3}{4}\cos\theta\right)2\dot{\theta}\ddot{\theta}\right)+\frac{3}{8}MgR\sin\theta \dot{\theta}=0$$
I used the approximation that $\sin\theta \approx \theta$ and $\cos\theta \approx 1$ and got:
$$\frac{3}{4}\theta\dot{\theta}^2+\frac{13}{10}\ddot{\theta}+\frac{3g}{8R}\theta=0$$
But it doesn't seem that it would be an oscillatory motion. I fed the above equation to wolfram alpha but got nothing. :(

Well, which is the actual question? Both make sense.

I don't see how the frictionless surface makes sense. If the CM doesn't displace from its position, how is it supposed to oscillate?

 

[consciousness]

$$\frac{3}{4}\theta\dot{\theta}^2+\frac{13}{10}\ddot{\theta}+\frac{3g}{8R}\theta=0$$
But it doesn't seem that it would be an oscillatory motion. I fed the above equation to wolfram alpha but got nothing. :(

This proves that the motion isn't simple harmonic (even for small displacements). To get a solution we need to solve that DE. If its any consolation, you have solved the physics part. Only the mathematics is left

I don't see how the frictionless surface makes sense. If the CM doesn't displace from its position, how is it supposed to oscillate?

For a frictionless surface, consider what happens when you displace the hemisphere angularly and allow it to oscillate. The gravitational force will act downwards on the COM and the normal reaction will act upwards (below the center of the base). I think it will be an SHM (easier than this question)

 

[Saitama]

For a frictionless surface, consider what happens when you displace the hemisphere angularly and allow it to oscillate. The gravitational force will act downwards on the COM and the normal reaction will act upwards (below the center of the base). I think it will be an SHM (easier than this question)

Isn't this the same case we are discussing currently in this thread?

 

[ehild]

Differentiating wrt time,
$$\frac{dE}{dt}=\frac{1}{2}MR^2\left(\frac{3}{4}\sin\theta\dot{\theta}^3+\left(\frac{7}{5}-\frac{3}{4}\cos\theta\right)2\dot{\theta}\ddot{\theta}\right)+\frac{3}{8}MgR\sin\theta \dot{\theta}=0$$
I used the approximation that $\sin\theta \approx \theta$ and $\cos\theta \approx 1$ and got:
$$\frac{3}{4}\theta\dot{\theta}^2+\frac{13}{10}\ddot{\theta}+\frac{3g}{8R}\theta=0$$
But it doesn't seem that it would be an oscillatory motion. I fed the above equation to wolfram alpha but got nothing. :(

Keep the terms linear in theta. (Ignore the first term).

ehild

 

[Saitama]

Keep the terms linear in theta. (Ignore the first term).

ehild

But that's $\dot{\theta}^2$, not $\theta^2$.

 

[haruspex]

Yes, you are right, it gets really simple with that. I got:
$$E=\frac{1}{2}MR^2\left(\frac{7}{5}-\frac{3}{4}\cos\theta\right)\left(\frac{d\theta}{dt}\right)^2+mgR\left(1-\frac{3}{8}\cos\theta\right)$$

Next I would approximate the cos(θ) terms as 1-θ²/2. The first one you can just approximate as 1 since it has a factor $\dot \theta^2$, which will be small. The 'base' energy is 5mgR/8, which gets rid of the the 1 in the approximation for the second cos:
$E=\frac{1}{2}MR^2\left(\frac{7}{5}-\frac{3}{4}\right)\left(\frac{d\theta}{dt}\right)^2+mgR\left(\frac{3}{16}\theta^2\right)$
But you're right, it's not SHM. Solution would involve inverse trig functions. So.. onto the frictionless version?

I don't see how the frictionless surface makes sense. If the CM doesn't displace from its position, how is it supposed to oscillate?

With no friction, the CoM will just bob up and down instead of (mostly) rocking from side to side. The point of contact will still move from side to side, but not as far.

 

[voko]

$E=\frac{1}{2}MR^2\left(\frac{7}{5}-\frac{3}{4}\right)\left(\frac{d\theta}{dt}\right)^2+mgR\left(\frac{3}{16}\theta^2\right)$
But you're right, it's not SHM.

$\dot x^2 + c^2 x^2 = c^2 A^2 \Rightarrow x = A \sin \left( ct + k \right)$. Not SHM?

 

[voko]

But that's $\dot{\theta}^2$, not $\theta^2$.

When we use the small oscillation approximation for energy, we take the term that is constant in displacement and quadratic in the derivative of displacement from kinetic energy, and the term that is quadratic in displacement from potential energy. That always leads to SHM. Displacement above means whatever our dynamic variable is, which is an angle in this particular case.

The above should have been explained to you in the course of your studies. You need to review that.

 

[Saitama]

When we use the small oscillation approximation for energy, we take the term that is constant in displacement and quadratic in the derivative of displacement from kinetic energy, and the term that is quadratic in displacement from potential energy. That always leads to SHM. Displacement above means whatever our dynamic variable is, which is an angle in this particular case.

The above should have been explained to you in the course of your studies. You need to review that.

Thanks a lot voko and haruspex!

I still don't understand why is it ok to approximate one of the cos as 1 and the other as $1-\theta^2/2$.

The only book I currently have is Kleppner and I don't think there is any discussion about the above approximations. :(

 

[voko]

Kleppner explains why you need to have the terms quadratic in "displacement" from potential energy. It does not say much about kinetic energy, except assuming it must in general have the form $k \dot x^2$. This is essentially what I wrote: "constant in displacement". More generally, it will be $k(x) \dot x^2$. For small oscillations, we retain only the lowest degree non-vanishing non-constant terms of expansions; those happen to be quadratic in $x$ for potential energy, and $k(0) \dot x^2$ for kinetic energy.

 

[Saitama]

Kleppner explains why you need to have the terms quadratic in "displacement" from potential energy. It does not say much about kinetic energy, except assuming it must in general have the form $k \dot x^2$. This is essentially what I wrote: "constant in displacement". More generally, it will be $k(x) \dot x^2$. For small oscillations, we retain only the lowest degree non-vanishing non-constant terms of expansions; those happen to be quadratic in $x$ for potential energy, and $k(0) \dot x^2$ for kinetic energy.

Got it, thanks voko! :)

 

[haruspex]

$\dot x^2 + c^2 x^2 = c^2 A^2 \Rightarrow x = A \sin \left( ct + k \right)$. Not SHM?

Yes, I realized my mistake somewhere in the middle of the night. Thanks.

 

[Tanya Sharma]

Hi Pranav...

The problem is comparatively easier and mathematics less tedious if you work with instantaneous axis of rotation .

That's just my two cents .

 

[Saitama]

Hi Pranav...

The problem is comparatively easier and mathematics less tedious if you work with instantaneous axis of rotation .

That's just my two cents .

Hi Tanya!

Completely agreed, that was much easier, thanks a lot.