Pappus Theorem and Ellipsoid Fig One: Is My Integral Approach Correct?

[LCSphysicist]

Homework Statement

Be the set of points (x,y) which "figure one".
And in the semiplane y >= 0.
Show the volume of the solid obtained by rotation about the axis x, of the set A, is equal to the product of the area of the ellipsoid with the circumference generated in the rotation of the center (alpha,beta) of the ellipsoid

Relevant Equations

All below

fig one:

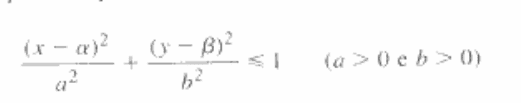
I just want to know if i am right in attack this problem by this integral:

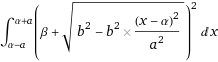*pi

Anyway, i saw this solution:

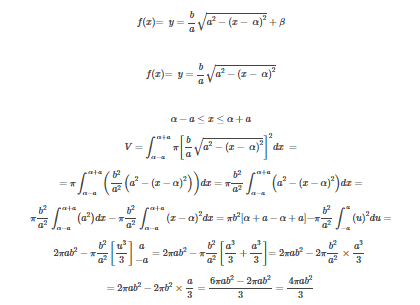
In which it cut beta, don't know why.

So i don't know.

 

[andrewkirk]

The result you are asked to prove will not be true if the ellipse intersects the x-axis at more than one point, ie if $\beta<b$. You can easily see that by considering the case where $\beta=0$ so the ellipse centre is on the x axis. The formula will give zero but the solid of revolution has positive volume.

Assuming $\beta\ge b$ the integral you suggest will not give the volume of the solid of revolution, which will be a squashed torus. It will give the volume of the convex hull of that torus. That is, it will include the space encircled by the torus as if it were part of the solid. To remove that space you need to deduct the other branch of the square root function from your integrand, which will then become:

$$\left(\beta + \frac ba\sqrt{a^2 - (x-\alpha)^2}\right)
- \left(\beta - \frac ba\sqrt{a^2 - (x-\alpha)^2}\right)$$

Examine this formula for the integrand and you will see why $\beta$ disappears.

 

[LCSphysicist]

The result you are asked to prove will not be true if the ellipse intersects the x-axis at more than one point, ie if $\beta<b$. You can easily see that by considering the case where $\beta=0$ so the ellipse centre is on the x axis. The formula will give zero but the solid of revolution has positive volume.

Assuming $\beta\ge b$ the integral you suggest will not give the volume of the solid of revolution, which will be a squashed torus. It will give the volume of the convex hull of that torus. That is, it will include the space encircled by the torus as if it were part of the solid. To remove that space you need to deduct the other branch of the square root function from your integrand, which will then become:

$$\left(\beta + \frac ba\sqrt{a^2 - (x-\alpha)^2}\right)
- \left(\beta - \frac ba\sqrt{a^2 - (x-\alpha)^2}\right)$$

Examine this formula for the integrand and you will see why $\beta$ disappears.

Hi, i returned to this question because i just remember now zz sorry
I tried again, and i almost get the result, but my integral was a little different.

While i am integrating:

f(x) is the positive root and f(x') is the negative root which you said.

The beta remains!

Seems to me the solution are integrating

Why am i wrong yet, I think i am not being able to visualize

 

[andrewkirk]

You are correct, and I was wrong. The beta does not disappear.

We can rewrite your (correct) integral as:
$$V = \int_{\alpha - a}^{\alpha+a} \pi\left(
\left(\beta + \frac ba\sqrt{a^2 - (x-\alpha)^2}\right)^2
- \left(\beta - \frac ba\sqrt{a^2 - (x-\alpha)^2}\right)^2
\right)\,dx$$
We expand the two squares and cancel, to get:
$$
= 4\pi\beta\frac ba \int_{\alpha - a}^{\alpha+a}
\sqrt{a^2 - (x-\alpha)^2}
\,dx
$$
Dividing by the circumference mentioned in the OP, which is $2\pi\beta$, gives:
$$
= 2\frac ba \int_{\alpha - a}^{\alpha+a}
\sqrt{a^2 - (x-\alpha)^2}
\,dx
$$
So it remains to prove that that is the area of the ellipse (which I think would be pretty straightforward).