- #1
Peter_Newman
- 155
- 11
Hello all,
I am currently working on the four fundamental spaces of a matrix. I have a question about the orthogonality of the
In the book of G. Strang there is this nice picture of the matrices that clarifies the orthogonality. This is what I mean:
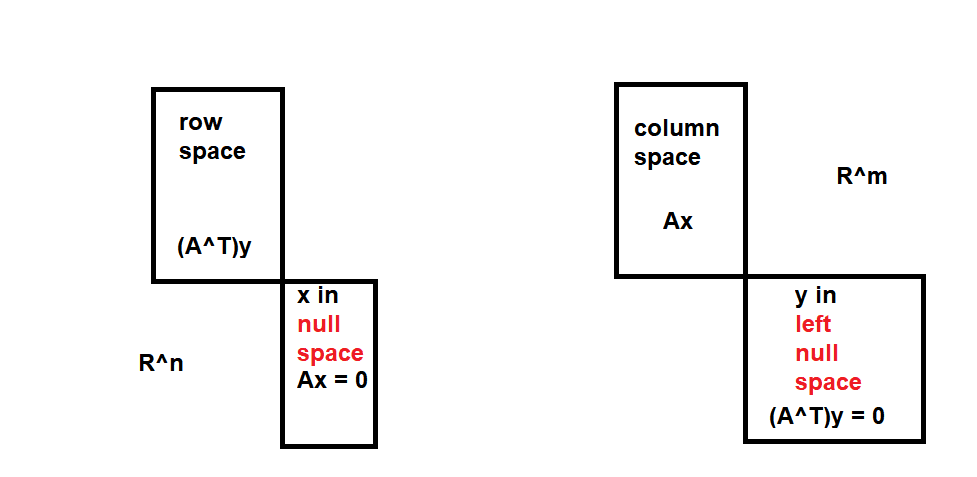
With the help of these expressions, this is then argued:
$$Ax = \begin{pmatrix}\text{row 1} \\ ... \\ \text{row m}\end{pmatrix}\begin{pmatrix} \vdots \\ x \\ \vdots \end{pmatrix} = 0$$
$$A^Ty = \begin{pmatrix}\text{transposed column 1 of A} \\ ... \\ \text{transposed column n of A}\end{pmatrix}\begin{pmatrix} \vdots \\ y \\ \vdots \end{pmatrix} = 0$$
------------------------------------------------
There is also a matrix proof, and this is what I am very interested in. You can read my thoughts about it in the explanations below.
I have shown the whole thing as a picture. Using this picture I try to show the matrix proof.
1. proof for the orthogonality of the row space to the null space:
$$\langle\,A^Ty,x\rangle = x^T(A^Ty) = (Ax)^Ty = 0^Ty = 0$$
2. proof of the orthogonality of the column space to the left null space:
$$\langle\, Ax, y\rangle = (Ax)^Ty = x^T(A^Ty) = x^T0 = 0$$
I think that is correct so far, but I am not quite sure. Therefore I would be very happy about a confirmation or contra position :)
Note 1: I would like to be honest enough to say that I have also asked this question to others HERE. However, I did not receive an answer there, but I would like to refer to this fact. If Someone here gives an answer, I would like to refer to it. I hope that's ok, because I can no longer delete my question in the other forum, but here I promise myself more adequate help (At least this was always so in the past :) )...
Note 2: This is not a homework assignment. I'm just reading the book in parallel and am interested in this question.
I am currently working on the four fundamental spaces of a matrix. I have a question about the orthogonality of the
- row space to the null space
- column space to the left null space
In the book of G. Strang there is this nice picture of the matrices that clarifies the orthogonality. This is what I mean:
With the help of these expressions, this is then argued:
$$Ax = \begin{pmatrix}\text{row 1} \\ ... \\ \text{row m}\end{pmatrix}\begin{pmatrix} \vdots \\ x \\ \vdots \end{pmatrix} = 0$$
$$A^Ty = \begin{pmatrix}\text{transposed column 1 of A} \\ ... \\ \text{transposed column n of A}\end{pmatrix}\begin{pmatrix} \vdots \\ y \\ \vdots \end{pmatrix} = 0$$
------------------------------------------------
There is also a matrix proof, and this is what I am very interested in. You can read my thoughts about it in the explanations below.
I have shown the whole thing as a picture. Using this picture I try to show the matrix proof.
1. proof for the orthogonality of the row space to the null space:
- The row space vectors are combinations ##A^Ty## of the rows, therefore the dot product of ##A^Ty## with any ##x## of the null space must be zero:
$$\langle\,A^Ty,x\rangle = x^T(A^Ty) = (Ax)^Ty = 0^Ty = 0$$
2. proof of the orthogonality of the column space to the left null space:
- The column space vectors are combinations ##Ax## of the columns, therefore the dot product of ##Ax## with any ##y## of the left null space must be zero:
$$\langle\, Ax, y\rangle = (Ax)^Ty = x^T(A^Ty) = x^T0 = 0$$
I think that is correct so far, but I am not quite sure. Therefore I would be very happy about a confirmation or contra position :)
Note 1: I would like to be honest enough to say that I have also asked this question to others HERE. However, I did not receive an answer there, but I would like to refer to this fact. If Someone here gives an answer, I would like to refer to it. I hope that's ok, because I can no longer delete my question in the other forum, but here I promise myself more adequate help (At least this was always so in the past :) )...
Note 2: This is not a homework assignment. I'm just reading the book in parallel and am interested in this question.