- #1
eleventhxhour
- 74
- 0
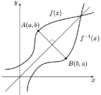
If (a, b) = f, then (b, a)= f^-1. The claim has been made that the graph of the inverse of a function is the mirror image of the function, reflected in the line y = x. To prove this you must
a) Show that the line that passes through the points (a, b) and (b, a) intersect the line y = x at a right angle.
b) Show that the distances between each point and the line y = x are the same. (To do this you MIGHT have to determine the point of intersection of the line passing though (a, b) and (b, a) and the line y = x).
Please help! I know that you can't really graph it on here, but it'd be so much help if you explained what the question means and how to solve it. I really don't understand it, so any sort of help would be really appreciated. Thanks!
a) Show that the line that passes through the points (a, b) and (b, a) intersect the line y = x at a right angle.
b) Show that the distances between each point and the line y = x are the same. (To do this you MIGHT have to determine the point of intersection of the line passing though (a, b) and (b, a) and the line y = x).
Please help! I know that you can't really graph it on here, but it'd be so much help if you explained what the question means and how to solve it. I really don't understand it, so any sort of help would be really appreciated. Thanks!