Proving Lemma 3.3 of L&S: Further Aspects of the Proof

[Math Amateur]

I am reading Chapter 3: Jordan Measure ... of Miklos Laczkovich and Vera T Sos's book "Real Analysis: Series, Functions of Several Variables, and Applications" (Springer) ...

I need help with some further aspects of the proof of Lemma 3.3 ... ... in order to fully understand the proof ...

The statement and proof of Lemma 3.3 of L&S reads as follows:

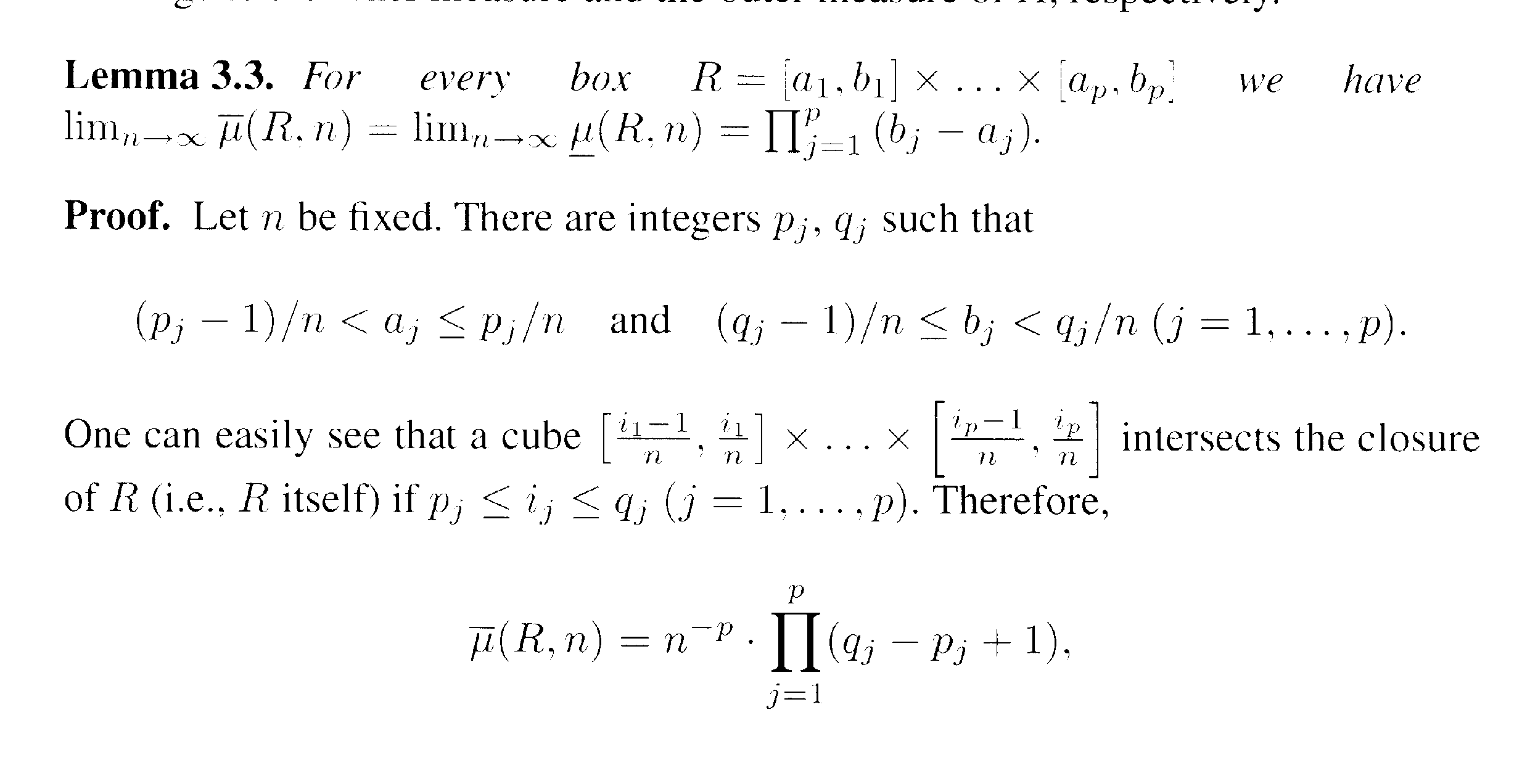
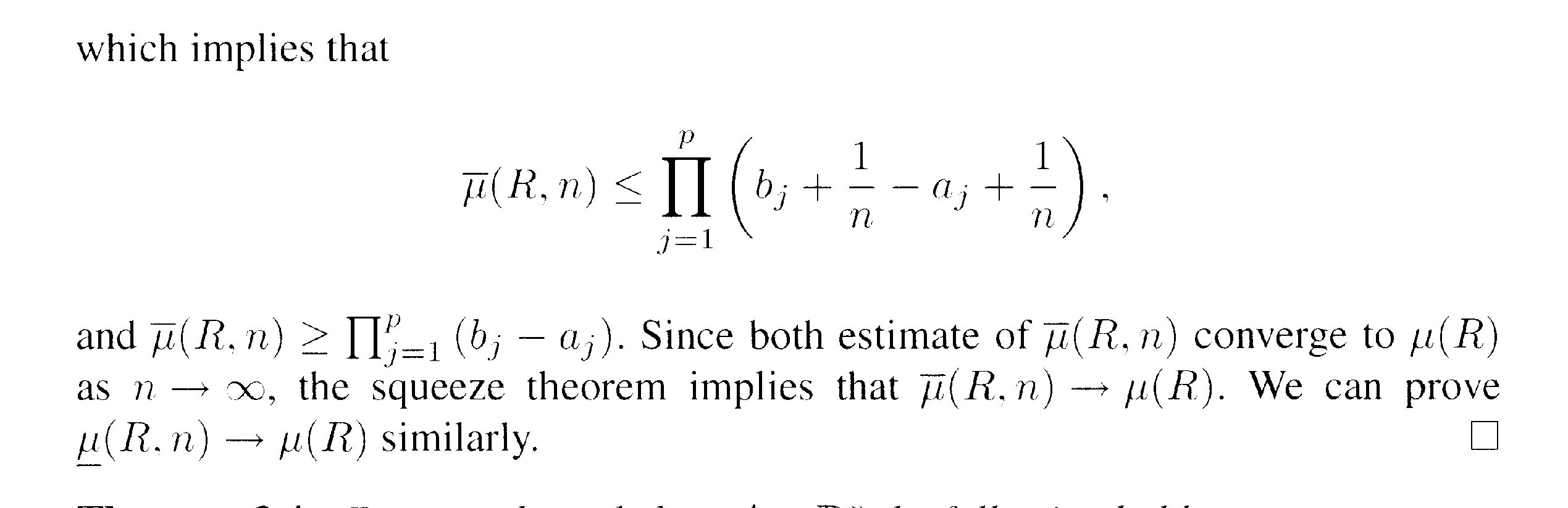
QUESTION 1

In the above proof by L&S we read the following:

" ... ... Let n be fixed. There are integers \(\displaystyle p_j, q_j \) such that

\(\displaystyle \frac{p_j - 1}{n} \lt a_j \leq \frac{p_j}{n} \text{ and } \frac{q_j - 1}{n} \lt b_j \leq \frac{q_j}{n} \)

... ... ... ... "
I tried several numerical examples ... and the examples indicated the above was true ...

... BUT ... ...How do we prove that there exist integers \(\displaystyle p_j, q_j \) such that

\(\displaystyle \frac{p_j - 1}{n} \lt a_j \leq \frac{p_j}{n} \text{ and } \frac{q_j - 1}{n} \lt b_j \leq \frac{q_j}{n} \)

... ... ... ...

QUESTION 2

In the above proof by L&S we read the following:

" ... ... One can easily see that a cube \(\displaystyle [ \frac{ i_1 - 1 }{n} , \frac{ i_1 }{n} ] \ \times \ldots \ \ldots \times \ [ \frac{ i_p - 1 }{n} , \frac{ i_p }{n} ] \) intersects the closure of R ( i.e. R itself) if \(\displaystyle p_j \leq i_j \leq q_j \) (j = 1, ... ... p) ... ...

I am unsure of how to visualize this ...

... ... ... can someone please explain how to formally and rigorously prove that a cube \(\displaystyle [ \frac{ i_1 - 1 }{n} , \frac{ i_1 }{n} ] \ \times \ldots \ \ldots \times \ [ \frac{ i_p - 1 }{n} , \frac{ i_p }{n} ] \) intersects the closure of R ( i.e. R itself) if \(\displaystyle p_j \leq i_j \leq q_j \) (j = 1, ... ... p) ... ... Help with the above two questions will be much appreciated ...

Peter
NOTE:

To make sense of Lemma 3.3 readers of the above post will need access to pages 95-97 of L&S so I providing this text as follows:

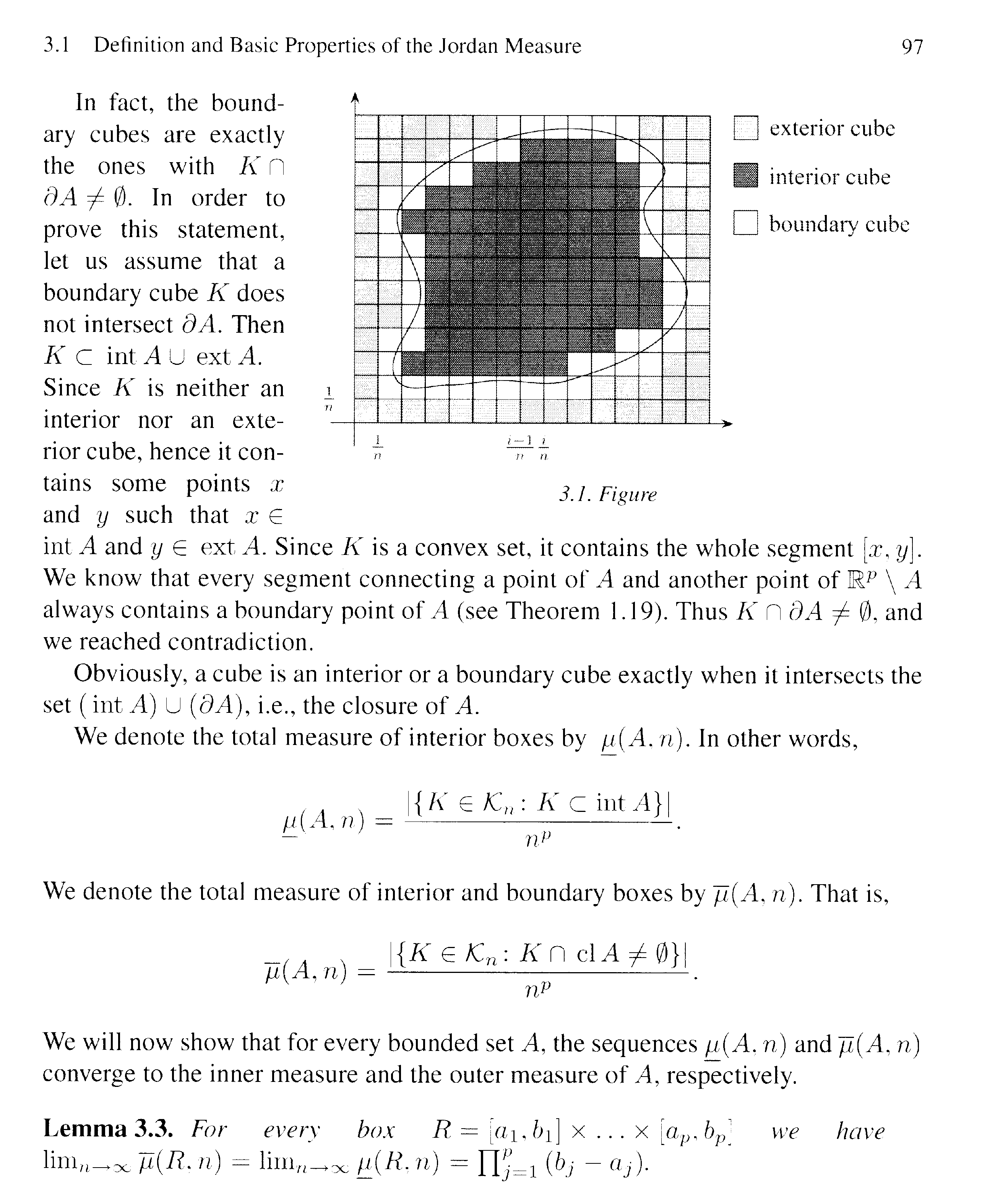
Hope that helps,

Peter

 

[GJA]

Hi Peter

Question 1

I will prove the existence of $p_{j}$; the argument for $q_{j}$ is similar.

Since the integers are not bounded above, the set $\{p\in\mathbb{Z}\, : \, na_{j}\leq p\}$ is non-empty. By the well-ordering principle, $\{p\in\mathbb{Z}\, : \, na_{j}\leq p\}$ has a least element. Let $p_{j}$ be this least element. Then $p_{j}-1< na_{j}\leq p_{j}\,\Longleftrightarrow\,\dfrac{p_{j}-1}{n}< a_{j}\leq\dfrac{p_{j}}{n}.$

Question 2

Since $p_{j}\leq i_{j}\leq q_{j}\,\Longrightarrow\, na_{j}\leq i_{j}$ and $i_{j}-1\leq nb_{j}$. We must examine two cases.

Case 1: $na_{j}\leq i_{j} \leq nb_{j}$

If this is the case, we are done because $\dfrac{i_{j}}{n}\in \left[\dfrac{i_{j}-1}{n}, \dfrac{i_{j}}{n} \right]\cap [a_{j}, b_{j}]$.

Case 2: $nb_{j} < i_{j}$

In this case, we use $i_{j}-1\leq nb_{j}$ from above. Then $\dfrac{i_{j}-1}{n}\leq b_{j} < \dfrac{i_{j}}{n}\,\Longrightarrow\, b_{j}\in \left[\dfrac{i_{j}-1}{n}, \dfrac{i_{j}}{n} \right]\cap [a_{j}, b_{j}]$.

Feel free to let me know if anything remains unclear.

 

[Math Amateur]

Thanks so much for your help GJA …

Still reflecting on what you have written …

… thanks again,

Peter