Q re de Sitter–Schwarzschild metric

[Buzz Bloom]

TL;DR Summary

I need some help with the notation in the equations in the Wikipedia article about the title subject.

The equations below are from

https://en.wikipedia.org/wiki/De_Sitter–Schwarzschild_metric#Metric .​

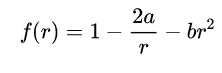
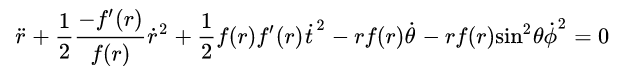
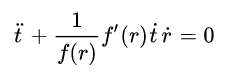
I am familiar with the dot on top of a variable as meaning d/dt, and the apostrophe as meaning d/dr (in this context). The dot on top of t, however, does not make any sense. I hope someone will explain this notation to me.

I am interested in the radial motion of a test particle relative to a black hole in a de Sitter universe. I want to compare this motion with the motion using just the Schwartzchild metric. Consequently the two terms involving θ and φ are irrelevant.

I am guessing that the dot might mean d/ds, but if that is correct, I would like to have it confirmed. The variable s is on the LHS of the metric in the form ds².

 

[Ibix]

The dot on top of t, however, does not make any sense. I hope someone will explain this notation to me.

It's the derivative of coordinate time with respect to an affine parameter along the particle's path. For a massive particle, this will usually be picked to be the particle's proper time. For a massless particle, you have to use a different parameter since proper time isn't defined along such paths.

 

[Buzz Bloom]

Hi Ibix:

Thank you for your post. The test particle I have in mind is not massless.

I found a definition for the derivative of proper time as

dτ = ds/c .​

https://en.wikipedia.org/wiki/Proper_time​

Therefore the dot means c×d/ds. Is this correct?

Regards,
Buzz

 

[Ibix]

Not exactly. $ds^2$ is defined for any path between two infinitesimally separated events. $d\tau$ is specifically for the path you are following. There is a distinction between differentiating with respect to "distance" along some path that may not be the one of interest and differentiating with respect to "distance" along the path you are talking about - you want the latter.

Differentiating with respect to $s$ isn't precisely wrong, as long as you are aware that you are not quite using the general definition of $s$. It's better to use $\tau$, since it should prompt you to be aware that your results relate to a particular path along which the proper time is $\tau$.

 

[Buzz Bloom]

Hi Ibix:

The path is unknown. That is what I am trying to solve for. The path can be defined different ways. For example: r(t), r(s), r(τ). Can you recommend how I should interpret the dot? How does the "affine parameter" fit into the problem?

I looked up

https://encyclopediaofmath.org/wiki/Affine_parameter .​

The terminology is unfamiliar to me. For example:

A parameter on a curve which is preserved under transformations of the affine group, for the determination of which the derivatives of the position vector of the curve of the lowest order must be known.​

I looked up affine group.

https://en.wikipedia.org/wiki/Affine_group​

In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.​

This is way over my head.

Regards,
Buzz

 

[Ibix]

Can you recommend how I should interpret the dot?

The way I said in post #2. It's $d/d\tau$ for a massive particle.

How does the "affine parameter" fit into the problem?

The proper time of a massive particle is an affine parameter along its path. You only need to worry about the more general definitions if you are thinking about null paths.

In space, marks on a piece of string mark off an affine parameter (distance) along the string. In spacetime, clock ticks along a timelike worldline mark off an affine parameter (proper time) along the worldline.

 

[Buzz Bloom]

Hi Ibix:

Since τ is absent from the three equations I am working with, if I cannot use

d/dτ = c×d/ds​

what can I use to get τ into the three equations. ds appears in the metric, so adding the metric equation works with d/ds.

The metric:

ds² = -f(r)dt² + (1/f(r)) dr²​

becomes:

1 = -f(r) (dt/ds)² + (1/f(r)) (dr/ds)² ,​

f(r) = -f²(r) (dt/ds)² + (dr/ds)² .​

Regards,
Buzz

 

[Ibix]

The point is that at some time τ on the particle's clock it is at coordinates $t(\tau),r(\tau),\theta(\tau),\phi(\tau)$. So $t$, $r$, $\theta$ and $\phi$ are (in this context) functions of $\tau$. Hence $\dot t=\frac{dt(\tau)}{d\tau}$, and $f'(r)=\frac{df}{dr}=\frac{2a}{r^2}-2br$. This gives you a rather nasty-looking system of differential equations.

 

[pervect]

Hi Ibix:

Since τ is absent from the three equations I am working with, if I cannot use

d/dτ = c×d/ds​

Tau is not actually absent from these equations. They are omitted, but implied. More on this later.

The equations you reference are also derived using the assumption that c=1. This can be inferred from the metric, i.e.

$$ds^2 = -f(r) dt^2 + \frac{dr^2}{f(r)} + r^2\,(d\theta^2 + \sin^2 \theta d\phi^2 ) $$

If c were not one, the metric would have included c as it was in the wiki article https://en.wikipedia.org/w/index.php?title=Schwarzschild_metric&oldid=985535994

$$ds^2 = -c^2 d\tau^2 = -(1-\frac{r_s}{r}) c^2 dt^2 + (1-\frac{r_s}{r}) ^ {-1} dr^2 + r^2 (d\theta^2 + \sin^2 \theta d\phi^2)$$

I've actually made minor edits to both wiki articles as a close inspection will show, in the interest of more
consistent notation between the two articles. Wiki isn't a textbook, they don't have consistent notation between articles, they're not written by the same people.

Back to the issue of $\tau$. Aside from the issue of setting c=1, which is a common simplification that the wiki article made but didn't mention in one of the two cases, there are some issues with your interpretation of the geodesic equation, which is what your question was about, I think.

The clearest way to address this is to re-write these equations fully, without abbreviations, I think.

For instance, the geodesic equation that you cite as

$$\ddot{t} + \frac{1}{f(r)} f'(r) \dot{t} \dot{r} = 0$$

should be interpreted as meaning

$$r = r(\tau) \quad t = t(\tau)$$
$$ \frac{ d^2 t(\tau)}{d\tau^2} + \frac{1}{f(r)} \frac {df(r)}{dr} \frac{dt(\tau)}{d\tau} \frac{dr(\tau)}{d\tau} = 0$$

You may be interested in finding r(t) - at least that's my assumption - but what the equations are actually giving you is $r(\tau)$ and $t(\tau)$.

$\tau$, as others have mentioned, is an affine parameter. For a massive particle, it's also proper time. Hopefully you're familiar with the concept of proper time from previous discussions.

 

[Buzz Bloom]

Hi Ibix:

Thank you very much for your post. I now feel much more confident that I am understanding what I am trying to do.

I have a memory regarding the distinction between proper time (τ) and observer time (t) I would like to confirm. The difference is based on the slowing down effect (also causing red shifts of emitted photons) due to gravitational time dilation on proper time. As the moving clock gets very far away from the mass making the gravitational field, the difference between the two clocks' ticks (assuming identical clocks) becomes very small. Is this correct?

Regards,.
Buzz

 

[PeterDonis]

have a memory regarding the distinction between proper time (τ) and observer time (t)

$t$ is not "observer time". It is coordinate time. Coordinates are just numerical labels for events. They have no physical meaning. What the relationship is between coordinate time and proper time along some observer's worldline will depend on which worldline it is and which spacetime geometry you are talking about.

 

[pervect]

To expand on what Peter said - not only is "t" just a label , it's not a very good label. The problems occur at the event horizon.

The reason the Schwarzschild or Scwharzschild-deSitter t coordinate is not a good label is that that some events on the horizon get an infinite number of different "t" coordinate labels, while other events are not labelled at all.

This is known technically as "a coordinate singularity".

Another examples of coordinate singularites are the r=0 point in polar coordinates. In this case, all points do have at least one (r,$\theta$) label, but the point at r=0 has an infinite number of $\theta$ labels rather than a unique label.

Proper time is the sort of time an un-adjusted atomic clock measures. A good model of proper time is that the clock is started at some event, and stopped at another event, at which point the clock reads the time interval between the two events. The clock needs to be physically present at both events.

 

[Ibix]

I have a memory regarding the distinction between proper time (τ) and observer time (t) I would like to confirm. The difference is based on the slowing down effect (also causing red shifts of emitted photons) due to gravitational time dilation on proper time. As the moving clock gets very far away from the mass making the gravitational field, the difference between the two clocks' ticks (assuming identical clocks) becomes very small. Is this correct?

As others have commented, $t$ is coordinate time, which is just a label. Typically, increasing values of $t$ do correspond in some way to increasing values on clocks, but the relationship is not as straightforward as you seem to think. And, as @pervect notes, sometimes there is no such relationship.

A relevant analogy is the relationship of longitude change to distance travelled. A 1° longitude change near the equator is a very different thing from near the pole, and the actual distance also depends on the latitude change, not just the longitude. Actually at the pole, a change of longitude doesn't even make sense.

Similarly, a 1s change in $t$ coordinate only has the straightforward relationship to elapsed time for some observer that you quoted if the other coordinates for that observer are held constant. If the observer is changing their spatial coordinates as well, it's more complex. Handling that (i.e. relating the coordinate time and the free-falling observer's proper time generally) is one part of what the geodesic equation is doing.

 

[Buzz Bloom]

To expand on what Peter said - not only is "t" just a label , it's not a very good label. The problems occur at the event horizon.

Similarly, a 1s change in coordinate only has the straightforward relationship to elapsed time for some observer that you quoted if the other coordinates for that observer are held constant.

Hi pervect and Ibix:

I had an understanding about t being a useful way to think about time if it was in terms of an observer located at a fixed position at an infinite radius (or perhaps a very large radius might be OK). If this is correct, then it produces a description in terms of r(t) of a radial motion for a test particle as seen by a stationary observer very far away along the same radius. In particular I am interested in motion moving radially away at some distance from the black hole, so there is no issue about the event horizon. Does this make sense?

If you are interested, I could explain my motivation for this exploration. It's a rather long story, and it might not be of any interest for you.

Regards,
Buzz

 

[pervect]

Hi pervect and Ibix:

I had an understanding about t being a useful way to think about time if it was in terms of an observer located at a fixed position at an infinite radius (or perhaps a very large radius might be OK). If this is correct, then it produces a description in terms of r(t) of a radial motion for a test particle as seen by a stationary observer very far away along the same radius. In particular I am interested in motion moving radially away at some distance from the black hole, so there is no issue about the event horizon. Does this make sense?

If you are interested, I could explain my motivation for this exploration. It's a rather long story, and it might not be of any interest for you.

Regards,
Buzz

The de-Sitter Schwarzschild coordinates will have issues when f(r) = 1 - 2a/r - br^2 is zero, and additionally of course at r=0 at the central singularity.

There will be two values of r where f(r) = 0, one of which is when r is small, one in which r is large. When r is small, we can often assume that the 1/r term dominates the r^2 term, and we find that with this approximation f(r)=0 when 1 - 2a/r is zero. This is the event horizon the same as the Schwarzschild metric. When r is large, we can often assume that the r^2 term dominates the 1/r term, and find the "cosmological horizon" when 1-br^2=0. The coordinates should be OK to use in the region between the event horizon and the cosmological horizon. You'll have bad behavior when f(r)=0. You'll have other issues if you work inside the event horizon or outside the cosmological horizon. To oversimplify, inside the event horizon or outside the cosmological horizon, the "t" coordinate will represent space, rather than time.

It's probably is best if you talk about your motivation some.

If you actually want to solve the geodesic equations, it's probably helpful to note that one of the geodesic equations, the one for $\ddot{t}$, is equivalent to:

$$\frac{d}{d\tau} \left( f(r) \frac{dt}{d\tau} \right) = 0$$

By the chain rule this expands to

$$\frac{df}{dr} \frac{dr}{d\tau} \frac{dt}{d\tau} + f(r) \frac{d^2 t}{d\tau^2} = 0$$ which as you'll note is equivalent one of the geodesic equations - just divide both sides by f(r).

This implies we can set $f(r) \frac{dt}{d\tau} = E$, where E is some constant.

 

[Buzz Bloom]

This implies we can set f(r)dt/dτ=E , where E is some constant.

Hi pervect:

This is very helpful. If I have not made any error,
$$dτ = \frac {Edr} {1-2a/r-br^2} .$$
If I cannot integrate this directly, I can do so numerically to get τ(r), the inverse of r(τ).

My motivation deals with my discontent with the use of the Newtonian escape velocity to determine a limiting distance from a gravitational mass for a test particle being gravitational bound.
$$ r = (2GM/H^2)^{1/3}$$
This does not take into account the influence of dark energy.

Regards,
Buzz

 

[PeterDonis]

my discontent with the use of the Newtonian escape velocity to determine a limiting distance from a gravitational mass for a test particle being gravitational bound

Where is this being done and who is doing it?

 

[PeterDonis]

This does not take into account the influence of dark energy.

Note that in Schwarzschild-de Sitter spacetime (and in de Sitter spacetime more generally), the notion of "escape velocity" actually doesn't make any sense, since de Sitter spacetime is not asymptotically flat, and asymptotic flatness is required for the notion of "escape velocity" to make sense.

 

[Buzz Bloom]

. . . asymptotic flatness is required for the notion of "escape velocity" to make sense.

Hi Peter:

There seems to be no end to the surprises.

I am interpreting this as also saying that if the universe is finite and hyper-spherical, then "escape velocity" does not make sense in that context either. Is this correct? If not, please help me understand the distinction.

In the absence of "escape velocity" is there an alternative criterion to calculate gravitational boundedness with the presence of dark energy (or the cosmological constant).

Regards,
Buzz

 

[Buzz Bloom]

Where is this being done and who is doing it?

Hi Peter:

I remember participating in a thread (about a year ago more-or-less) in which I was attempting to use a criterion for calculating the specific influence of the expansion on circular orbits. I have tried to relocate this thread, but so far I have failed. You participated in that thread, trying to explain to me why my idea was faulty. My idea involved using (what I named as) the Hubble acceleration equaling the gravitational acceleration, and I obtained a criterion for a distance D equal to 1/2 the distance based on escape velocity equaling HD.

Regards,
Buzz

 

[PeterDonis]

I am interpreting this as also saying that if the universe is finite and hyper-spherical, then "escape velocity" does not make sense in that context either. Is this correct?

Yes.

I remember participating in a thread (about a year ago more-or-less) in which I was attempting to use a criterion for calculating the specific influence of the expansion on circular orbits. I have tried to relocate this thread, but so far I have failed. You participated in that thread

I remember the thread; I'll see if I can find it.

 

[PeterDonis]

In the absence of "escape velocity" is there an alternative criterion to calculate gravitational boundedness with the presence of dark energy (or the cosmological constant).

I'm not sure what you mean by "gravitational boundedness", unless it is basically what we were discussing in that previous thread you referred to.

 

[Buzz Bloom]

I'm not sure what you mean by "gravitational boundedness", unless it is basically what we were discussing in that previous thread you referred to.

Hi: Peter:

My memory of the old thread is not clear about details. As I remember the discussion, the concept is that the expansion of the universe has no influence on the trajectories of two bodies if they have stable orbits. (At that time, as I remember it, the concept that dark energy can influence the orbits was not discussed.) This is because the two bodies are bound to each other by their gravitational influence on each other, and there is a maximum distance the orbits can take the two bodies from each other. The concept of escape velocity was used to calculate a maximum distance between the two bodies such that at a greater distance D the velocity HD could influence to some extent (not necessarily adding HD as a velocity) such that the effected trajectories move the two bodies apart without limit in a flat universe. At that time the discussion did not include consideration of a finite universe, or any non-flat universe.

Regards,
Buzz

 

[PeterDonis]

the concept is that the expansion of the universe has no influence on the trajectories of two bodies if they have stable orbits

This is basically true, but let me restate it in a more precise form.

Suppose we want to model our solar system as it is "embedded" in the universe as a whole. In order to do that, we have to "paste together" two different spacetime geometries. Basically, our model will be that we have a spherical "bubble", containing the solar system, in which the spacetime geometry is the Schwarzschild geometry; and this "bubble" will be embedded in the universe as a whole, whose spacetime geometry is the FRW geometry. At the boundary of the "bubble", which we can think of as some spherical surface that is at a radius from the Sun of, say, 1 light-year, the two geometries have to match, which involves some technical mathematical conditions that I don't think we need to go into detail about here.

In a model of this type, the fact that we have spherical symmetry in both regions (the Schwarzschild region inside the "bubble" and the FRW region outside) means that we can invoke the shell theorem, which says that, if we have a spherical "bubble" with a spherically symmetric spacetime outside it (in this case, the FRW region describing the rest of the universe), the spacetime geometry outside the "bubble" has no effect at all on the spacetime geometry inside the "bubble".

Translated into more concrete physical terms, this means that the expansion of the universe (which is a property of the FRW spacetime geometry outside the "bubble") has no effect on the orbits of objects in the solar system (which is a property of the spacetime geometry inside the "bubble").

Of course our real universe does not exactly satisfy the idealized assumptions of the idealized model described above. But the fact that we can use the Schwarzschild geometry (or more precisely a power series approximation to it, called the post-Newtonian approximation) to make very accurate predictions regarding the orbits of objects in the solar system means that, in fact, the idealized model I described is an extremely accurate approximation--that in fact it is true even in our real universe that the expansion of the universe, the spacetime geometry outside the solar system, has no effect on the orbits of objects inside the solar system.

At that time, as I remember it, the concept that dark energy can influence the orbits was not discussed.

I don't think it was at first, but IIRC it was later on in the discussion. If I can find the thread I'll post a link to it here.

Adding dark energy to the idealized model I described above is actually pretty straightforward, and doesn't change the basic answer I gave above. The key difference between dark energy and the rest of the stress-energy in the universe is that we cannot assume that the density of dark energy inside the solar system is exactly zero. In the idealized model above, when we used the Schwarzschild geometry to model the region inside the "bubble", where the solar system is, that was equivalent to assuming that there is no other stress-energy in that region, aside from the Sun itself (we are here treating the planets and everything else as test objects, with no effect on the spacetime geometry; relaxing that assumption doesn't change the basic answer, it just complicates the details of how we predict the actual orbits of objects inside the solar system). In other words, we were assuming that the uniform density in the FRW model of the universe as a whole stops at the boundary of the "bubble", and vacuum begins.

In the presence of dark energy, we can no longer make that assumption, because dark energy has the same density literally everywhere--not just as an approximation on large distance scales, as for the ordinary matter and energy in the universe as it is represented in the FRW geometry, but literally everywhere. That means that, to include dark energy in our idealized model, we have to use for the region inside the "bubble", not the Schwarzschild geometry, but the Schwarzschild-de Sitter geometry.

It turns out, however, that the only thing that changes inside the "bubble" when we do that is that the orbits of objects are slightly different (because, heuristically, the inward "acceleration due to gravity" of the Sun is slightly offset by the outward "acceleration" due to dark energy, so the situation is as if the Sun's mass were slightly smaller than it actually is, with appropriate changes to all orbital parameters). But it is still true that those orbits are not affected by the spacetime geometry outside the bubble--which includes the expansion of the universe. The orbits are affected by the dark energy inside the bubble (more precisely, by the dark energy that is closer to the Sun than the orbiting object is), but they are not affected by the dark energy outside the bubble any more than they are affected by anything else outside the bubble.

 

[pervect]

Hi pervect:

This is very helpful. If I have not made any error,
$$dτ = \frac {Edr} {1-2a/r-br^2} .$$
If I cannot integrate this directly, I can do so numerically to get τ(r), the inverse of r(τ).

My motivation deals with my discontent with the use of the Newtonian escape velocity to determine a limiting distance from a gravitational mass for a test particle being gravitational bound.
$$ r = (2GM/H^2)^{1/3}$$
This does not take into account the influence of dark energy.

Regards,
Buzz

This doesn't look right to me.

Compare it to the Schwarzschild case, which is well known, and which is a special case of the de-Sitter Schwarzschild metric (henceforth dss metric) with b=0.

https://www.fourmilab.ch/gravitation/orbits/ has essentially the same treatment as my text, MTW, for the Schwarzschild case, though the online treatment isn't as detailed and may be too hard to follow on its own :(.

The forumilab treatment include the case where there is non-radial motion, but that's an unnecessary complication for what I think you want. We can get rid of the non-radial motion by setting the constant L in the forurmilab treatment to 0.

We also need to consider that our metric uses a, and their metric uses M. We also need to note that their $\tilde{E}$ is the same as our E when we use a unit test mass. This later point is a fine one, it's mostly about the physical interpretation of E as energy.

Then for the Schwarzschid case we get

$$ \left( \frac{dr}{d\tau} \right)^2 = (E^2 - 1) + 2a/r$$

where E is some constant. This doesn't match what you get above, you do not have any square roots. "Escape" velocity is that velocity where $\frac{dr}{d\tau} = 0$ at r =infinity, which imples that E=1 at "escape velocity".

So we are left with

$$\frac{dr}{d\tau} = \sqrt{\frac{2a}{r}}$$

for the case where b=0 (the Schwarzschild case) and the object is at "escape velocity". Your analysis should duplicate this result when b=0. You'll probably want to define your notion of "escape" velocity as reaching the cosmological horizon with zero velocity.

It's also worth noting that $\frac{dr}{d\tau}$ is a coordinate velocity, it's not the sort of velocity a local observer would measure.

What you'll need to duplicate this result is the result for $dt / d\tau$ that I gave previously, and the fact that norm of the 4-velocity is -1, i.e. that with the dss metric given previously

$$-f(r) \left( \frac{dt}{d\tau} \right) ^2 + \frac{1}{f(r)} \left( \frac{dr}{d\tau} \right) ^2 = -1$$

 

[pervect]

Hi: Peter:

My memory of the old thread is not clear about details. As I remember the discussion, the concept is that the expansion of the universe has no influence on the trajectories of two bodies if they have stable orbits. (At that time, as I remember it, the concept that dark energy can influence the orbits was not discussed.) This is because the two bodies are bound to each other by their gravitational influence on each other, and there is a maximum distance the orbits can take the two bodies from each other. The concept of escape velocity was used to calculate a maximum distance between the two bodies such that at a greater distance D the velocity HD could influence to some extent (not necessarily adding HD as a velocity) such that the effected trajectories move the two bodies apart without limit in a flat universe. At that time the discussion did not include consideration of a finite universe, or any non-flat universe.

Regards,
Buzz

I should add a caution about generalizing from the dss metric we've been discussing.

The overview here is that the Schwarzschild metric is static, and so is the dss metric, which is equivalent to saying that we having time translation symmetry, manifest by the fact that none of the coordinates depend on time.

The cliff notes version of this is that the metric determines the orbits, the metric coefficients don't depend on time, therefore the orbits don't depend on time.

However, the actual cosmology with dark matter, the FLRW cosmology, isn't so nicely behaved. The metric coefficients do depend on time. The FLRW metric is idealized over a global average with no clumping. In this global average, the density of normal matter and dark matter both decrease with time, and hence the resulting metric does depend on time.

Of course, the existence of the solar system illustrates that the FLRW model is an idealization, an average. We actually have clumping of matter.

The analysis is complicated by the fact that we don't have a good handle on the dark matter content (if any) present in the solar system, and it's behavior with time.

What I have read, though, is that it is generally felt that the most significant effect in our actual solar system as far as "losing matter" goes is the radiation of energy away by the sun, in the form of radiation and the solar wind of charged particles of various sorts.

Other effects exist, for instance the total energy in the cosmic microwave background contained in the volume of the solar system goes down due to cosmological redshift, but it and they are tiny effects compared to the loss of mass from the solar system via other mechanisms.

If the solar system were at the cosmological average, as much stuff would come in and went out, but it's not at the average, so more stuff goes out than comes in.

A more complex question is the effect of the distribution of matter outside the solar system on the orbits. Birkhoff's theorem says that with perfect spherical symmetry, there would be no effect. There might be some tiny effect due to the lack of perfect spherical symmetry, but I have never seen anyone try to quanify that, nor demonstrate an even theoretical existence of such an effect.

So, when we focus on the issue, we focus on the matter in the solar system. There's no reason to believe that the distribution of matter outside the solar system would affect its overal size, and some reasons to think that it shouldn't.

 

[Buzz Bloom]

Hi @perfect:

Thank you very much for your very thoughtful last two posts. I will take me a while to digest them, so I won't be responding about them for a while.

Regards,
Buzz

 

[PeterDonis]

the actual cosmology with dark matter, the FLRW cosmology, isn't so nicely behaved. The metric coefficients do depend on time.

That's because of a different coordinate choice, which does not make the timelike Killing vector field of de Sitter (or de Sitter Schwarzschild) spacetime manifest. But that doesn't make the timelike KVF go away; it just means it isn't manifest in those particular coordinates.

The underlying issue here is that the "static slicing" of de Sitter spacetime is different from any of the FLRW slicings that are commonly used (the flat one is the one used in the Lambda CDM model, since our best current model says the universe is spatially flat; but there are also open and closed slicings). When we describe the entire universe including dark energy, we are using the flat de Sitter slicing; but when we describe a single gravitating object in the presence of dark energy, we are using the static de Sitter slicing. The choice of slicing is a convenience for description, but, as I said above, the timelike KVF is still there in both cases. So a model of an isolated gravitating system like the solar system that makes use of such a timelike KVF is still perfectly valid even though the universe as a whole is expanding.

The FLRW metric is idealized over a global average with no clumping. In this global average, the density of normal matter and dark matter both decrease with time, and hence the resulting metric does depend on time.

But the density of dark energy does not depend on time. And inside the "bubble" I described that we can use as the boundary of our model of the solar system embedded in the rest of the universe, none of the other ordinary matter in the universe is there, and we can, at least as a first approximation, assume that there is negligible dark matter there as well.

Even if we did assume that there was non-negligible dark matter in the solar system, that still would not require that its density within the "bubble" we are using to model the solar system would change with time. After all, that dark matter is part of a larger gravitationally bound system, our galaxy (and perhaps even the cluster of galaxies of which our galaxy is a part). The decrease with time of the density of normal matter and dark matter in the standard FLRW model is not because individual pieces of ordinary matter or dark matter are "thinning out"; it is because the average distance between the pieces is increasing. Any model of just one of those individual pieces, as an isolated object (the model I have been describing of the solar system is such a model) can thus ignore the expansion of the universe, at least to a very good approximation.

it is generally felt that the most significant effect in our actual solar system as far as "losing matter" goes is the radiation of energy away by the sun, in the form of radiation and the solar wind of charged particles of various sorts.

This is my understanding as well. The effects of that loss of mass-energy, AFAIK, are expected to be negligible on time scales we can directly measure. I don't know that I've seen any estimates of what the effects would be on cosmological time scales (say a billion years).

 

[pervect]

That's because of a different coordinate choice, which does not make the timelike Killing vector field of de Sitter (or de Sitter Schwarzschild) spacetime manifest. But that doesn't make the timelike KVF go away; it just means it isn't manifest in those particular coordinates.

I haven't found a definitive reference, oddly enough, but what I did find matches my recollection, that the FLRW metric has spatial Killing vectors arising from spatial translation symmetries, and rotational symmetries, but none representing time translation symmetries, for a total of 6 space-like Killing vectors.

See for instance https://physics.stackexchange.com/questions/261075/symmetry-group-of-flrw-metric

If the FLRW metric did have timelike Killing vectors, we'd be able to talk about the energy of a FLRW universe, and I don't believe that's possible.

The methods I espoused in earlier posts certainly rely on having a time-like Killing vector to make E a constant number and define a time-independent escape velocity. I don't believe that the existence of spatial Killing vector fields can provide an alternate replacement, in general if the metric lacks the required symmetry with regards to time, the velocity needed to reach the cosmological horizon will depend on the time coordinate as well as the position coordinates.

As far as the expansion of the solar system goes, my post is based on my recollections of a paper by Cooperstock and others, mentioned by Ned Wright in his cosmology FAQ http://www.astro.ucla.edu/~wright/cosmology_faq.html#SS

Why doesn't the Solar System expand if the whole Universe is expanding?

This question is best answered in the coordinate system where the galaxies change their positions. The galaxies are receding from us because they started out receding from us, and the force of gravity just causes an acceleration that causes them to slow down, or speed up in the case of an accelerating expansion. Planets are going around the Sun in fixed size orbits because they are bound to the Sun. Everything is just moving under the influence of Newton's laws (with very slight modifications due to relativity). [Illustration] For the technically minded, Cooperstock et al. computes that the influence of the cosmological expansion on the Earth's orbit around the Sun amounts to a growth by only one part in a septillion over the age of the Solar System. This effect is caused by the cosmological background density within the Solar System going down as the Universe expands, which may or may not happen depending on the nature of the dark matter. The mass loss of the Sun due to its luminosity and the Solar wind leads to a much larger [but still tiny] growth of the Earth's orbit which has nothing to do with the expansion of the Universe. Even on the much larger (million light year) scale of clusters of galaxies, the effect of the expansion of the Universe is 10 million times smaller than the gravitational binding of the cluster.

Unfortunately the LANL website was down for maintenance when I wrote this, so I couldn't review the Cooperstock paper, just Ned Wright's comments.

 

[PeterDonis]

the FLRW metric has spatial Killing vectors arising from spatial translation symmetries, and rotational symmetries, but none representing time translation symmetries, for a total of 6 space-like Killing vectors.

This is true for an FLRW metric with nonzero density of matter or radiation. It is not true for de Sitter spacetime, however, even though de Sitter spacetime admits coordinate choices that put the metric into FLRW form.

For our actual universe, which is currently dark energy dominated but has nonzero density of matter and energy, there is no global timelike KVF as there is in de Sitter spacetime, although as the universe becomes more and more dark energy dominated, there will be a better and better approximation to one.

However, in a local region like the "bubble" I described, where we are assuming that there is no matter or radiation (other than the single central mass), the vacuum portion can be described exactly by Schwarzschild-de Sitter spacetime, which does have the timelike KVF. So within the "bubble", that KVF is in fact present. In the global geometry, the "bubble" appears as a "world tube" with a boundary that has a constant proper surface area; the timelike KVF only exists in the region inside the boundary.

The methods I espoused in earlier posts certainly rely on having a time-like Killing vector to make E a constant number and define a time-independent escape velocity.

Yes, and in the "bubble" model I described, that means "escape" cannot be defined as "escape to infinity", but only as "escape to the boundary of the bubble". If we pick, say, a 1 light-year radius sphere around the Sun as our "bubble", the difference in escape velocities will be extremely small and the ordinary treatment of "escape velocity" in a stationary spacetime will be an extremely good approximation.

 

[PeterDonis]

I remember the thread; I'll see if I can find it.

Found it:

https://www.physicsforums.com/threa...distance-between-two-spherical-shells.989533/

 

[pervect]

If I haven't made some error, it looks like the geodesic equations for the dss metric should boil down to
$$\dot{t} = \frac{E}{f(r)} \quad \dot{r} = \sqrt{E^2-f(r)}$$

It'd take more work to write $\dot{t}$ and $\dot{r}$ as a function of $\tau$, however, so it's difficult to directly confirm that these are the correct solutions as-is. I imagine one could use the chain rule, but I haven't done this.

Here E is some constant, representing the energy, and f(r) is, as previously
$$f(r) = 1 - \frac{2a}{r} - br^2$$

It looks like the motion is best understood by the effective potential technique, as used by MTW and on the forurmilab website for the Schwarzschild case, and that the effective potential $V^2(r)$ is just f(r). When b=0, this matches the Schwarzschild effective potential $1-2a/r$ from the fourmilab site / MTW as it should.

The forumilab website is https://www.fourmilab.ch/gravitation/orbits/

a and b are somewhat inconvenient parameter, I wound up normalizing the event horizon to occur at at r=1, and the cosmologcal horizon at r=C, where C is some constant, and then solves for a and b.

Plotting the effective potential for C=10, I get something that looks like this.

If the object can reach the peak of the effective potential at $r=\sqrt[3]{55} \approx 3.8$, with a coordinate velocity $dr/d\tau$ greater than 0, it will reach the cosmological horizon (and continue on to infinity). I've stop the graph at the cosmological horizon as the coordinates are too confusing beyond it.

 

[PeterDonis]

it will reach the cosmological horizon (and continue on to infinity)

Actually, there is no "infinity" in Schwarzschild-de Sitter spacetime. It is not asymptotically flat. Schwarzschild spacetime is, but Schwarzschild-de Sitter can be thought of, heuristically, as a finite piece of Schwarzschild, centered on the black hole, "glued" to de Sitter spacetime with a finite size spherical "world tube" taken out. So the asymptotic structure of Schwarzschild-de Sitter spacetime is the same as that of de Sitter spacetime. That means there is no "infinity" in the sense of "escape to infinity". The best you can do, relative to the black hole, is to "escape" beyond the cosmological horizon.

 

[pervect]

Actually, there is no "infinity" in Schwarzschild-de Sitter spacetime. It is not asymptotically flat. Schwarzschild spacetime is, but Schwarzschild-de Sitter can be thought of, heuristically, as a finite piece of Schwarzschild, centered on the black hole, "glued" to de Sitter spacetime with a finite size spherical "world tube" taken out. So the asymptotic structure of Schwarzschild-de Sitter spacetime is the same as that of de Sitter spacetime. That means there is no "infinity" in the sense of "escape to infinity". The best you can do, relative to the black hole, is to "escape" beyond the cosmological horizon.

I'll amend my results to omit any statements about what happens after the cosmological horizon, then, since I haven't really analyzed that case.

I'd need some more information to fully appreciate your point, I think. Do you have any references you could share? Aditionally, would you agree that the horizon is a point of no return, that the test particle, once beyond the horizon, does not return to the central mass, nor can signals from the test particle return? You mention an analogy to a sphere. Are there any CTC's in the de-Sitter spacetime? I know there are CTC's in the anti-de-Sitter space time. But I didn't think there were any in the de-Sitter spacetime, though I haven't seen anything definitive.

Additionally, do you have any comment about the solution I found to the geodesic equations, and/or the effective potential diagram?

 

[PeterDonis]

I'd need some more information to fully appreciate your point, I think. Do you have any references you could share?

Section 2 of the following paper has a good overview of the geometric and conformal properties of de Sitter spacetime:

https://arxiv.org/pdf/hep-th/0110007.pdf

Note in particular the Penrose diagram in Fig. 2. Unlike asymptotically flat spacetimes, which have a spacelike infinity to the side, and separate timelike and null infinites to the past and future (with the timelike being at the bottom and top, and the null being at an angle between the timelike and the spacelike), de Sitter spacetime has only two infinities, one to the past (at the bottom) and one to the future (at the top), and there is no distinction between timelike and null (both kinds of curves reach the same infinities).

The rest of that section has other good diagrams showing how various commonly used coordinate charts cover de Sitter spacetime, and what portions they cover.

The Penrose diagram of Schwarzschild-de Sitter spacetime is even more interesting, as shown in Fig. 1 of this paper:

https://arxiv.org/pdf/1007.3851.pdf

Note how there are still no spacelike or separate null infinities; instead there is an infinite "row" of alternating Schwarzschild and de Sitter regions.

One thing I have not been able to find is a diagram for gravitational collapse of an object to a black hole in a universe that is asymptotically de Sitter instead of asymptotically flat--i.e., a version of the classic Oppenheimer-Snyder model set in de Sitter spacetime.