Quantum Mechanics Hydrogen Atom Expectation Value Problem

[cemtu]

Homework Statement

Expected Value of L^2 is needed

Relevant Equations

In a similar problem, similar way of solution is presented at attempted solution

I can not solve this problem:

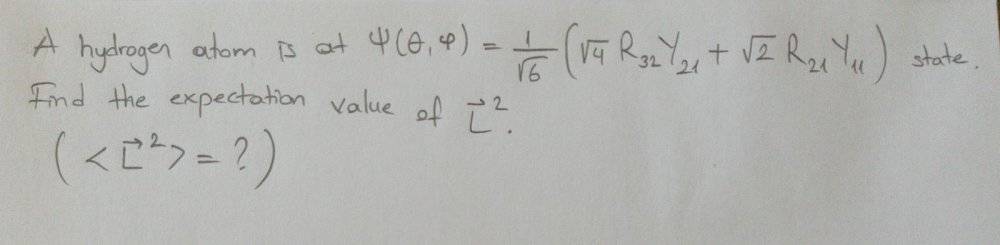
However, I have a similar problem with proper solution:

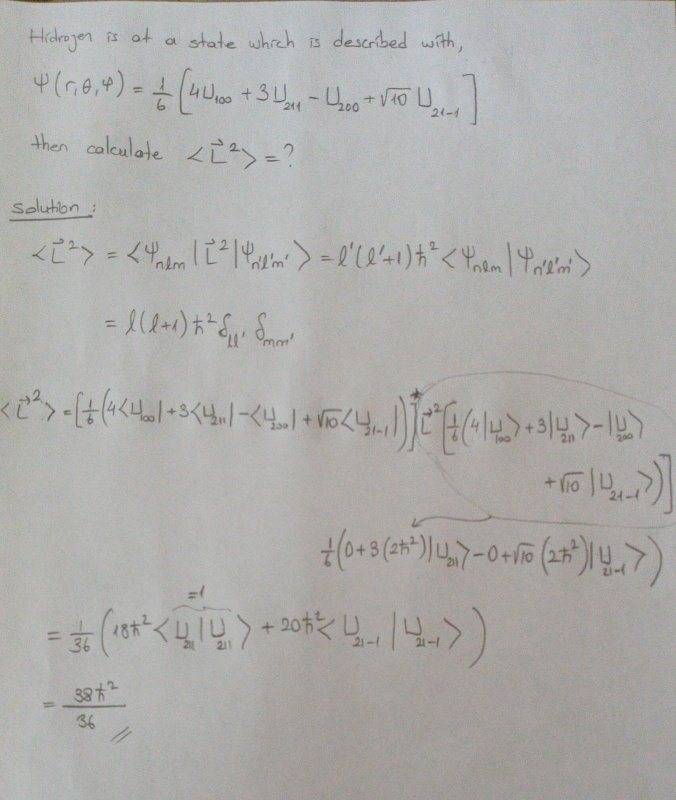
Can you please guide me to solve my question? I am not being able to relate Y R (from first question) and U (from second question), and solve the question at the top above...

 

[PeroK]

What do $Y_{21}$ and $Y_{11}$ tell you?

 

[cemtu]

What do Y21Y21 and Y11Y11 tell you?

In spherical harmonics it means:

 

[PeroK]

Okay, but what does that function represent (in terms of angular momentum)?

 

[cemtu]

Okay, but what does that function represent (in terms of angular momentum)?

They are joint eigenfunctions of L^2 and Lz, and they constitue an orthonormal basis in the Hilbert space.

 

[PeroK]

They are joint eigenfunctions of L^2 and Lz, and they constitue an orthonormal basis in the Hilbert space.

Okay, and what do the "11" and "21" mean?

 

[cemtu]

Okay, and what do the "11" and "21" mean?

21 means that " 2 is given for "l" and 1 is given for "m", both m and l are quantum numbers. And for 11, 1 is given for both m and l.

 

[PeroK]

21 means that " 2 is given for "l" and 1 is given for "m", both m and l are quantum numbers.

Okay, but what does $l = 2$ mean? Isn't that something to do with angular momentum?

 

[cemtu]

l=2 gives 5 different possible numbers for m, and corresponds to d orbital.

 

[PeroK]

l=2 gives 5 different possible numbers for m, and corresponds to d orbital.

Let me tell you the answer: $l = 2$ tells you the total angular momentum squared for that state. That's how the spherical harmonics arose in the first place - as eigenstates of angular momentum.

If you find a system in that state, then you know its angular momentum.

 

[cemtu]

Let me tell you the answer: $l = 2$ tells you the total angular momentum squared for that state. That's how the spherical harmonics arose in the first place - as eigenstates of angular momentum.

If you find a system in that state, then you know its angular momentum.

Okay.

 

[cemtu]

you can direct me more questions. I will try to answer all until the question is solved bit by bit.

 

[PeroK]

you can direct me more questions. I will try to answer all until the question is solved bit by bit.

How much angular momentum is associated with $Y_{11}$ and $Y_{21}$?

 

[cemtu]

How much angular momentum is associated with $Y_{11}$ and $Y_{21}$?

for $Y_{11}$ L and for $Y_{21}$ L^2 . Sorry sir but I couldn't think of, or find any answer in books(griffits) other than this.

 

[PeroK]

The $l$ quantum number is the eigenvalue of $L^2$ corresponding to $l(l+1)\hbar^2$.

 

[cemtu]

The $l$ quantum number is the eigenvalue of $L^2$ corresponding to $l(l+1)\hbar^2$.

okay. I am still here.

 

[kuruman]

So what is $$L^2\left[\frac{1}{\sqrt{6}}\left(\sqrt{4}R_{32}Y_{21}+\sqrt{2}R_{21}Y_{11}\right)\right]~?$$What do you get when you operate on the given wavefunction with $L^2$?

 

[cemtu]

can anyone please recommend me any source book to study this topic. Griffits Quantum book ain't doing good...

 

[PeroK]

can anyone please recommend me any source book to study this topic. Griffits Quantum book ain't doing good...

This is all covered in Griffiths (Chapter 4.3). That's where I learned QM. There are many other texts out there, but ultimately you have to understand the material.

 

[cemtu]

This is all covered in Griffiths (Chapter 4.3). That's where I learned QM. There are many other texts out there, but ultimately you have to understand the material.

On it.

 

[PeroK]

On it.

Let me summarise two important aspects of QM: eigenstates and superposition. I'll do this for AM (angular momentum), but the same ideas apply across QM generally.

An eigenstate (of AM) means that you get a single value of AM if you make a measurement on that state. The spherical harmonics $Y_{lm}$ are eigenstates of AM. If you have a system in this eigenstate and you measure AM you always get $l$ and $m$, which correspond to the values:
$$L^2 = l(l+1)\hbar^2, \ \text{and} \ L_z = m\hbar$$
Systems, however, can be in a superposition of eigenstates. In this case, you may get different values of AM, associated with the different eigenstates in the superposition. To some extent we can ignore the spatial wavefunction and focus on AM. For example, if you have the superposition:
$$aY_{l_1m_1} + bY_{l_2m_2}$$
Then the coefficients $a$ and $b$ tell you how likely the system is to be found in each eigenstate if AM is measured. The probabilities are, of course, $|a|^2$ and $|b|^2$. And, the AM you get in each case is $l_1, m_1$ and $l_2, m_2$.

The expected value of AM is then the statistical mean of: $l_1, m_1$ with probability $|a|^2$ and $l_2, m_2$ with probability $|b|^2$. For the expected value of $L^2$ this is:
$$\langle L^2 \rangle = |a|^2 l_1(l_1 + 1)\hbar^2 + |b|^2 l_2(l_2 + 1)\hbar^2$$

Note that you can derive this from the formal definition of expected value:
$$\langle L^2 \rangle = \langle \Psi | L^2 | \Psi\rangle$$
That's an important exercise to work through.

I hope this helps.

 

[DrClaude]

An eigenstate (of AM) means that you get a single value of AM if you make a measurement on that state. The spherical harmonics $Y_{lm}$ are eigenstates of AM. If you have a system in this eigenstate and you measure AM you always get $l$ and $m$, which correspond to the values:
$$L^2 = l(l+1)\hbar^2, \ \text{and} \ L_z = m\hbar$$

Let me be pedantic. The equation as written makes no sense, what @PeroK means is
$$L^2 Y_{lm} = l(l+1)\hbar^2 Y_{lm}, \ \text{and} \ L_z Y_{lm} = m\hbar Y_{lm}$$

 

[PeroK]

Let me be pedantic. The equation as written makes no sense, what @PeroK means is
$$L^2 Y_{lm} = l(l+1)\hbar^2 Y_{lm}, \ \text{and} \ L_z Y_{lm} = m\hbar Y_{lm}$$

I meant $L^2$ and $L_z$ as quantities, as opposed to operators.

 

[DrClaude]

I meant $L^2$ and $L_z$ as quantities, as opposed to operators.

Got it. But I never saw such a notation before.

 

[PeroK]

Got it. But I never saw such a notation before.

I guess if I were being pedantic I would put hats on the operators, to distiguish them from the observable quantities:
$$\langle L^2 \rangle = \langle \psi | \hat L^2 | \psi \rangle$$