Question about integration in physics

[EddiePhys]

I've always thought of integration as a way to solve differential questions. I'd solve physics problems involving calculus by finding the change in the function df(x) when I increment the independent variable (say x of f(x)) by an infinitesimal amount dx, attaching some physical significance to df = f(x+dx) - f(x) , writing a differential equation relating df and dx. This would give me f'(x) which I would integrate with respect to x to give me the function I was looking for.

I want to know why I can also look at integration as summing up of infinitesimal elements.

For e.g If I want to find the mass of a ring of mass M(redundant, I know) , I can do that by "summing up" infinitesimal elements of mass dm => \int {dm} from 0 to M or summing up \rho Rd\theta from 0 to 2\pi

Or if I want to find the total gravitational potential due to a ring:

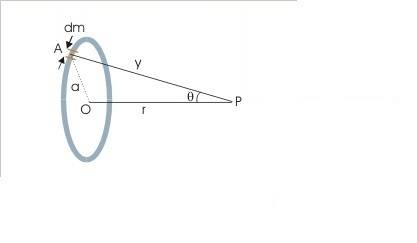
I could write the small potential dV for an element dm and sum up these dV's using integration to give me the total V due to the ring.

But I want to know why this works/makes sense, mathematically.
Because I think of integration either a way to solve differential equations or as the area under a curve, and I don't understand why the area under the curve(and which curve?) would represent the total potential V or mass M

 

[anorlunda]

Because I think of integration either a way to solve differential equations or as the area under a curve, and I don't understand why the area under the curve(and which curve?) would represent the total potential V or mass M

Come on, get serious. Why is your bank balance the integral of the deposits /withdrawals? Have you seen the video of Richard Feynman talking about "why" questions?

Why are you asking that question?

 

[fresh_42]

Maybe this Insight on the various forms of integration is of use to you:
https://www.physicsforums.com/insights/omissions-mathematics-education-gauge-integration/

Also of interest:
https://en.wikipedia.org/wiki/History_of_calculus
https://christober.wordpress.com/2008/07/17/integration-archimedes-method/

 

[A.T.]

I want to know why I can also look at integration as summing up of infinitesimal elements.

Seems more like a math question:
http://hyperphysics.phy-astr.gsu.edu/hbase/integ.html#c4

 

[fresh_42]

Seems more like a math question:
http://hyperphysics.phy-astr.gsu.edu/hbase/integ.html#c4

Thx. It really fits better into Calculus.

 

[EddiePhys]

could you show how I could apply the Riemann sum for the two examples i mentioned at the end? (mass and gravitational potential)

 

[pixel]

I'm not sure how you are thinking of "area." If you have a velocity that is a function of time and want to know the distance traveled in the time interval t₁ → t₂, then you would find the following integral between t₁ and t₂:

x = ∫v(t) dt

By doing so, you are calculating the "area" under the v(t) curve between those two limits.

 

[EddiePhys]

I'm not sure how you are thinking of "area." If you have a velocity that is a function of time and want to know the distance traveled in the time interval t₁ → t₂, then you would find the following integral between t₁ and t₂:

x = ∫v(t) dt

By doing so, you are calculating the "area" under the v(t) curve between those two limits.

i realized that thinking in terms of area will not help my intuition. could you show how I could apply the Riemann sum for the two examples i mentioned at the end? (mass and gravitational potential)

 

[Stephen Tashi]

Because I think of integration either a way to solve differential equations or as the area under a curve, and I don't understand why the area under the curve(and which curve?) would represent the total potential V or mass M

From the point of view of modern mathematics, thinking in terms of "infinitesimals" the way they are used in physics is not a reliable way to think. It is merely a way people think intuitively. (To think about "infinitesimals" in a reliable way, you can study a branch of mathematics called "Nonstandard Analysis", but that approach isn't likely to please anyone who isn't yet comfortable with the standard approach to calculus that employs limits.)

From an intuitive perspective, it is possible to understand a connection between taking antiderivatives and doing integrals. To do this, you need to think in terms of finite approximations to both derivatives and integrals.

Define the operator $D_{dx}$ acting on a function $F$ at the value $x$ to be:
$D_{dx} F(x) = \frac{ F(x+dx) - F(x)}{dx}$. Where $dx$ is a number, not an "infinitesimal". Then the approximate value of the derivative of $F(x)$ at the value $x$ is $F'(x) \approx D_{dx} F(x)$.

Let $g(x) = F'(x)$. Consider $\int_a^b g(x) dx$. Approximate this integral as a "regular" Riemann sum by partitioning $[a,b]$ into N intervals of length $dx$ (where $dx$ is a finite number, not an "infinitesimal).
The approximate value of the integral is

$\int_a^b g(x) dx \approx g(a)(dx) + g(a+dx)( dx) + g(a + 2dx)( dx) + ... g(a + (N-1)dx) (dx)$ .

where I have used the value of $g$ at the left hand endpoint of each interval to approximate its average value over whole interval. (This sum is the familiar approximation of an area under a curve using areas of rectangles.)

Now make a further approximation by approximating $g(.)$ with $D_{dx} F(.)$.

$\approx D_{dx} F(a) (dx) + D_{dx} F(a+dx) (dx) + D_{dx}F(a + 2dx) (dx) + ... +D_{dx} F(a + (N-1)dx) (dx)$ .

Now, replace $D_{dx} F(.)$ with its definition to reveal that it is the approximate derivative of $F(.)$.

$\int_a^b g(x) dx \approx \frac{F(a+dx) - F(a)}{dx} dx + \frac{F(a+2dx) - F(a+dx)}{dx} dx + ...+ \frac{ F(a + Ndx) - F(a+(N-1)dx}{dx} dx$

$= \frac{F(a+dx)-F(a)}{1} + \frac{F(a+2x)-F(a+dx)}{1} + \frac{F(a+3dx)-F(a + 2dx)}{1} + ...+ \frac{ F(a+(N-1)dx-F(a+(N-2))dx}{1} + \frac{F(a+Ndx)-F(a+(N-1dx)}{1}$where I've written out more terms of the sum to emphasize that it is a "telescoping" sum. Adding two consecutive terms like $\frac{F(a+2x) - F(a + dx)}{1}$ and $\frac{ F(a+3x) - F(a+2x)}{1}$ results in a simplification - due to fact that adding them includes cancellations like $F(a+2x) - F(a+2x)$.

After such simplifications, the total sum is just $F(a+(N-1)dx) - F(a)$.

If $F$ is a continuous function and $dx$ is a small number, then $a + (N-1)dx$ is within $dx$ of the value $b$. So the total sum is approximately $F(b) - F(a)$.

This suggests the value of the definite integral $\int_a^b g(x) dx$ is given by $F(b) - F(a)$ where $g(x) = F'(x)$. In other words, finding definite integral involves using $F(x)$, which is an antideriviative of $g(x)$.

This is not rigorous mathematics, but it shows the intuitive idea that the connection between integration and anti-differentiation is due to a telescoping sum. This form of intutition has do with patterns of algebraic manipulations rather than geometry or physics.

Telescoping sums are also useful in understanding finite summations. For example, finding a closed form expression of a summation like $\sum_{k=1}^n k^2$ can be approached as the problem of finding the "anti-difference" function for $k^2$. Find a function $F(k)$ such that $F(k+1) - F(k) = k^2$ Then $\sum_{k=1}^n k^2 = F(n+1) - F(1)$.

 

[EddiePhys]

From the point of view of modern mathematics, thinking in terms of "infinitesimals" the way they are used in physics is not a reliable way to think. It is merely a way people think intuitively. (To think about "infinitesimals" in a reliable way, you can study a branch of mathematics called "Nonstandard Analysis", but that approach isn't likely to please anyone who isn't yet comfortable with the standard approach to calculus that employs limits.)

From an intuitive perspective, it is possible to understand a connection between taking antiderivatives and doing integrals. To do this, you need to think in terms of finite approximations to both derivatives and integrals.

Define the operator $D_{dx}$ acting on a function $F$ at the value $x$ to be:
$D_{dx} F(x) = \frac{ F(x+dx) - F(x)}{dx}$. Where $dx$ is a number, not an "infinitesimal". Then the approximate value of the derivative of $F(x)$ at the value $x$ is $F'(x) \approx D_{dx} F(x)$.

Let $g(x) = F'(x)$. Consider $\int_a^b g(x) dx$. Approximate this integral as a "regular" Riemann sum by partitioning $[a,b]$ into N intervals of length $dx$ (where $dx$ is a finite number, not an "infinitesimal).
The approximate value of the integral is

$\int_a^b g(x) dx \approx g(a)(dx) + g(a+dx)( dx) + g(a + 2dx)( dx) + ... g(a + (N-1)dx) (dx)$ .

where I have used the value of $g$ at the left hand endpoint of each interval to approximate its average value over whole interval. (This sum is the familiar approximation of an area under a curve using areas of rectangles.)

Now make a further approximation by approximating $g(.)$ with $D_{dx} F(.)$.

$\approx D_{dx} F(a) (dx) + D_{dx} F(a+dx) (dx) + D_{dx}F(a + 2dx) (dx) + ... +D_{dx} F(a + (N-1)dx) (dx)$ .

Now, replace $D_{dx} F(.)$ with its definition to reveal that it is the approximate derivative of $F(.)$.

$\int_a^b g(x) dx \approx \frac{F(a+dx) - F(a)}{dx} dx + \frac{F(a+2dx) - F(a+dx)}{dx} dx + ...+ \frac{ F(a + Ndx) - F(a+(N-1)dx}{dx} dx$

$= \frac{F(a+dx)-F(a)}{1} + \frac{F(a+2x)-F(a+dx)}{1} + \frac{F(a+3dx)-F(a + 2dx)}{1} + ...+ \frac{ F(a+(N-1)dx-F(a+(N-2))dx}{1} + \frac{F(a+Ndx)-F(a+(N-1dx)}{1}$where I've written out more terms of the sum to emphasize that it is a "telescoping" sum. Adding two consecutive terms like $\frac{F(a+2x) - F(a + dx)}{1}$ and $\frac{ F(a+3x) - F(a+2x)}{1}$ results in a simplification - due to fact that adding them includes cancellations like $F(a+2x) - F(a+2x)$.

After such simplifications, the total sum is just $F(a+(N-1)dx) - F(a)$.

If $F$ is a continuous function and $dx$ is a small number, then $a + (N-1)dx$ is within $dx$ of the value $b$. So the total sum is approximately $F(b) - F(a)$.

This suggests the value of the definite integral $\int_a^b g(x) dx$ is given by $F(b) - F(a)$ where $g(x) = F'(x)$. In other words, finding definite integral involves using $F(x)$, which is an antideriviative of $g(x)$.

This is not rigorous mathematics, but it shows the intuitive idea that the connection between integration and anti-differentiation is due to a telescoping sum. This form of intutition has do with patterns of algebraic manipulations rather than geometry or physics.

Telescoping sums are also useful in understanding finite summations. For example, finding a closed form expression of a summation like $\sum_{k=1}^n k^2$ can be approached as the problem of finding the "anti-difference" function for $k^2$. Find a function $F(k)$ such that $F(k+1) - F(k) = k^2$ Then $\sum_{k=1}^n k^2 = F(n+1) - F(1)$.

I understood that the integral is the limiting case of a Riemann sum. But how do I set up such a sum in physics problems?

I know for a Riemann sum we need to sum up ∑f(x_i)Δx from i = 1 to ∞ and Δx ->0 turning this into an integral.

But for the two problems I'd given (finding the total mass and total gravitational potential energy) I've gotten M = ΣΔM and V = ΣGΔM/y but I have no idea how to proceed after this and set up the index on the sigma so I can turn this into an integral.

 

[Stephen Tashi]

I understood that the integral is the limiting case of a Riemann sum. But how do I set up such a sum in physics problems?

A typical scenario is:

Given: If variable_A is constant with respect to variable_B then "the answer" is (variable_A)(variable_B).

Conclude: When variable_A varies with respect to variable_B , the "total answer", as a function of variable_B, is $\int$variable_A with respect to variable_B. example: Displacement $d$ (i.e. "distance") = velocity $v$ times times elapsed time $t$ when $v$ is constant with respect to $t$. So when velocity $v(t)$ varies with time $t$, displacement $d(t) = \int_{0}^{t} v(t) dt.$

Justification by Riemann sums: Divide elapsed time up into $N$small subintervals $[t_0, t_0 + dt], [t_0 + dt, t_0 + 2 dt], ... ,[t0 + (N-1) dt, t0 + Ndt = t]$. On each interval $[t0 + k\ dt, t0 + (k+1)dt]$ , approximate $v(t)$ by using the constant value of $v(t0 + k\ dt)$ for that entire interval. The displacement over that interval is thus approximated by $v(k0+\ dt) (dt)$. The total displacement is thus $\sum_{k=1}^N v(t0+k\ dt) (dt)$, which is a Riemann sum approximating $\int_{t0}^{t} v(t)dt$.

For e.g If I want to find the mass of a ring of mass M(redundant, I know) , I can do that by "summing up" infinitesimal elements of mass dm => \int {dm} from 0 to M

example: When a rod of length $L$ has constant mass density $\rho$ per unit length, total mass $M = (\rho)(L)$.
Suppose the rod has a mass density $\rho(x)$ per unit length that varies with the position $x$ on the rod.
Then $M = \int_0^L \rho(x) dx$.

Justification by Riemann sums: Divide the total length $L$ of the rod up into $N$ sub-lengths $[0,0+dx], [0+dx,0+2dx],[0+2dx,0+3dx],...,[0+(N-1)dx, 0+Ndx = L]$. Approximate the mass density $\rho(x)$ on the interval $[0+k\ dx, 0+(k+1)dx]$ by its value $\rho(0+k\ dx)$ at the left hand endpont. The approximate mass of the interval is $\rho(0+k\ dx) (dx)$. The total mass is approximately $\sum_{k=0}^{k=N} \rho(0+k\ dx) (dx)$, which is a Riemann sum for $\int_{0}^{L} \rho(x) dx$.